Morphological Image Processing

1. Sets in Morphology and Their Representation

In mathematical morphology, objects in an image are represented as sets. In binary images, where pixels are either “on” (e.g., white) or “off” (e.g., black), we can define the set of “on” pixels as representing the object in question. These sets are subsets of the 2-D integer space $\mathbb{Z}^2$, meaning that each element of the set is a 2-D vector corresponding to the coordinates of a pixel.

For grayscale images, each pixel not only has spatial coordinates $(x, y)$ but also an intensity value $z$, making the representation a 3-tuple $(x, y, z)$. Sets in even higher-dimensional spaces may include other image attributes, such as color or time.

2. Reflection and Translation of Sets

Two fundamental operations in morphological processing are reflection and translation of sets, both of which are essential for defining morphological operations.

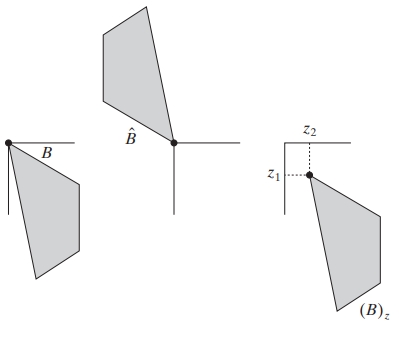
Reflection of a Set

The reflection of a set $B$, denoted $B^N$, is defined as:

In other words, if $B$ is a set of pixels (2-D points) representing an object in an image, then $B^N$ is simply the set of points in $B$ whose coordinates are replaced by their negatives $(-x, -y)$. This operation is illustrated in Figures 9.1(a) and 9.1(b) by a simple set and its reflection.

Translation of a Set

The translation of a set $B$ by a point $z$, denoted $B_z$, is defined as:

This means that if $B$ is a set of pixels representing an object in an image, then $B_z$ is the set of points in $B$ where each coordinate $(x, y)$ has been replaced by $(x + z_1, y + z_2)$, where $z = (z_1, z_2)$. Figure 9.1(c) illustrates this concept.

3. Structuring Elements (SEs)

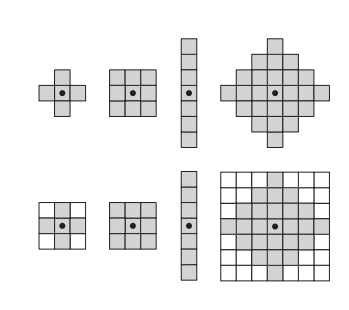
A structuring element (SE) is a small set or “probe” used to examine an image for properties of interest. Structuring elements are essential in morphology because they define the extent and pattern of transformations applied to an image. In practice, SEs are typically rectangular arrays, with each element representing a location that is either a part of or excluded from the SE. Figures 9.2(a) through (d) show examples of common SEs.

Each SE has an origin, usually marked by a dot, which serves as the reference point when the SE interacts with the image. For symmetric SEs, the origin is generally assumed to be at the center unless otherwise specified. When SEs are not rectangular, they are padded with background elements to form a rectangle. This padding is necessary to make operations such as dilation and erosion easier to implement computationally.

4. Basic Morphological Operations Using Structuring Elements

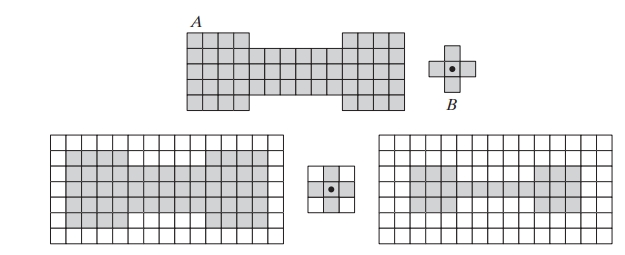
Consider a simple set $A$ and a structuring element $B$ as shown in Figures 9.3(a) and 9.3(b). Morphological operations are defined by moving the SE across the image so that its origin visits every pixel in $A$. At each position, the SE checks whether it is entirely contained within the set $A$.

1. Erosion: Erosion shrinks or “erodes” the boundaries of the set $A$ based on the structuring element $B$. Formally, erosion of $A$ by $B$, denoted $A \ominus B$, is defined as:

   $$A \ominus B = \{ z | B_z \subseteq A \}$$

   Here, $B_z$ is the translation of $B$ by $z$. Erosion retains only those pixels in $A$ where $B$ fits completely within $A$, resulting in a shrunken version of $A$.

2. Dilation: Dilation expands the boundaries of the set $A$ using the structuring element $B$. It is denoted by $A \oplus B$ and defined as:

   $$A \oplus B = \{ z | (B^N)_z \cap A \neq \emptyset \}$$

   Dilation places the SE at each pixel in $A$ and includes all locations where any part of $B$ overlaps with $A$, leading to an enlarged set.

5. Example of an Operation with Structuring Elements

Suppose we apply an operation on a binary image using a square SE. By sliding this SE over the image and marking each location where it fits entirely within the foreground pixels, we can effectively erode the shape of objects in the image, removing small irregularities. This can be useful for reducing noise or isolating object boundaries.

In Figure 9.3, we see how the structuring element interacts with the set $A$. When the SE’s origin is positioned on a border element, part of the SE extends beyond $A$, meaning it is no longer fully contained within $A$, which results in an eroded boundary.

6. Applications of Preliminaries in Morphology

The concepts of reflection, translation, and structuring elements form the foundation for more advanced morphological operations, such as opening and closing. These operations are essential in tasks such as:

• Noise reduction: Erosion and dilation can be combined to remove small noise elements while preserving overall structure.
• Boundary extraction: By using structuring elements that selectively highlight edges, morphological processing can identify object contours.
• Object segmentation: Morphology helps to separate objects from the background, facilitating object detection in computer vision.

Erosion and dilation are two foundational operations in morphological image processing. They are primarily used for shape analysis, noise reduction, boundary extraction, and object segmentation. Both operations are based on manipulating sets that represent objects within an image, often using a smaller shape called a structuring element (SE) to probe and modify the image.

1. Dilation

Dilation is a morphological operation that expands the boundaries of objects within an image. It is particularly useful for closing small gaps, connecting disjoint components, and filling in holes. In binary images, dilation adds pixels to the object boundaries, effectively growing the object. For grayscale images, it intensifies bright regions and can smooth transitions between pixel intensities.

Mathematical Definition of Dilation

Given a binary image represented as a set $A$ and a structuring element $B$, the dilation of $A$ by $B$, denoted by $A \oplus B$, is defined as:

In this definition:

• $B^N$ represents the reflection of the structuring element $B$.
• $(B^N)_z$ is the translation of $B^N$ by a point $z$.
• The operation $A \oplus B$ produces a new set that consists of all points $z$ where the reflected and translated structuring element $B$ overlaps with any part of $A$.

Dilation can also be defined in terms of supremum (maximum) for grayscale images. For a grayscale image $f(x, y)$ and a structuring element $B$, dilation is given by:

This operation means that each pixel in the output image is replaced with the maximum pixel value of the input image within the neighborhood defined by the structuring element.

Example of Dilation in Binary Images

Consider a binary image $A$ with the following 3×3 matrix and a 3×3 square structuring element $B$:

Binary Image $A$:

Structuring Element $B$:

To apply dilation, we position the center of $B$ over each pixel in $A$. At each position where $B$ overlaps with a pixel set to 1 in $A$, we set the central pixel of the new output to 1. After processing all positions, the output matrix becomes:

Dilated Output:

In this case, the structuring element connects and expands the object, filling in the gaps and growing the shape of the object.

2. Erosion

Erosion is the opposite of dilation; it shrinks or erodes the boundaries of objects in an image. Erosion is useful for eliminating small noise elements, separating connected components, and isolating distinct objects. In binary images, erosion removes pixels from the boundaries of objects, thereby reducing their size.

Mathematical Definition of Erosion

For a set $A$ (representing an object in a binary image) and a structuring element $B$, the erosion of $A$ by $B$, denoted $A \ominus B$, is defined as:

This means that erosion produces a set of points $z$ where the translated structuring element $B_z$ is entirely contained within $A$. In other words, the erosion operation will only retain the regions in $A$ where the entire structuring element fits within $A$ without crossing its boundaries.

For grayscale images, erosion can be defined in terms of infimum (minimum). If $f(x, y)$ is a grayscale image and $B$ is a structuring element, the erosion of $f$ by $B$ is given by:

This operation means that each pixel in the output image is replaced with the minimum pixel value within the neighborhood defined by $B$.

Example of Erosion in Binary Images

Using the same binary image $A$ and structuring element $B$ as before:

Binary Image $A$:

Structuring Element $B$:

In erosion, we place the center of $B$ over each pixel in $A$. For each position, if every pixel covered by $B$ is 1, we set the central pixel in the output to 1. Otherwise, we set it to 0. After processing, the eroded output becomes:

Eroded Output:

In this example, erosion reduces the size of the object, removing pixels from its boundary and isolating the central pixel.

3. Applications of Erosion and Dilation

Erosion and dilation form the basis of many other morphological operations and have practical applications in image processing:

• Noise Removal: Erosion can be used to eliminate small noise particles by eroding away single-pixel elements, while dilation can help restore the main object structure after noise removal.
• Boundary Extraction: By subtracting an eroded image from the original image, we can extract the boundary of an object.
• Hole Filling and Object Connection: Dilation is effective for filling small holes within objects or connecting fragmented object parts.

4. Combining Erosion and Dilation

When used together, erosion and dilation can be combined to perform more complex morphological operations:

• Opening: Erosion followed by dilation. This operation removes small objects and noise while preserving the shape and size of larger structures.
• Closing: Dilation followed by erosion. This operation fills small holes and connects nearby objects without significantly altering the size of the main object.

Opening and closing are essential operations in morphological image processing. Both techniques refine shapes within an image and have specific applications in noise reduction, contour smoothing, and shape analysis. Opening tends to smooth object contours by removing narrow connections or small protrusions, while closing smooths contours in a way that connects gaps, fills holes, and fuses breaks.

1. Opening

Opening is a morphological operation that involves the erosion of a set (or object) followed by a dilation using a structuring element. Opening is denoted by $A \circ B$, where:

• $A$ is the original set (often representing an object in an image).
• $B$ is the structuring element, a shape that defines the “probe” for the operation.

Mathematical Definition of Opening

The opening of a set $A$ by a structuring element $B$, denoted by $A \circ B$, is defined as:

In this formula:

1. $A \ominus B$: Erode $A$ by $B$ to shrink or refine the object boundaries.
2. $(A \ominus B) \oplus B$: Dilate the eroded result by $B$, effectively restoring the main part of the object without adding back the removed small protrusions or narrow connections.

This approach smooths the object by removing small, unwanted features that may not fit the structuring element.

Geometric Interpretation of Opening

Imagine rolling a flat “ball” with the shape of the structuring element $B$ along the inside boundary of $A$. The boundary points that the structuring element touches define the new boundary of $A \circ B$. As a result, the operation smooths out narrow protrusions or “isthmuses” and removes small features that the structuring element cannot entirely fit into.

For example, consider an object with a thin extension, such as a narrow “tail.” If the structuring element $B$ is a disk larger than this tail, opening will erode and remove the tail, smoothing the object.

Example of Opening in Binary Images

Suppose we have a binary image with a small, narrow feature:

Binary Image $A$:

Using a 2×2 square structuring element $B$:

Applying erosion to $A$ with $B$ would remove the small, narrow connection (tail) in the image. Subsequent dilation would restore the main body of the shape but not the removed tail.

Properties of Opening

Opening has the following properties:

1. Subset Property: $A \circ B \subseteq A$
   • The opening of a set by a structuring element will always be a subset of the original set.
2. Idempotence: $(A \circ B) \circ B = A \circ B$
   • Applying the opening operation multiple times with the same structuring element has no further effect beyond the first application.
3. Increasing Property: If $C \subseteq D$, then $C \circ B \subseteq D \circ B$
   • Opening preserves the subset relationship; a smaller set will produce a result contained within the opening of a larger set.

2. Closing

Closing is a morphological operation that involves dilation followed by erosion. Closing tends to smooth out small holes, fill narrow gaps, and bridge breaks in the contour of an object. It is denoted by $A \cdot B$, where $A$ is the original set and $B$ is the structuring element.

Mathematical Definition of Closing

The closing of a set $A$ by a structuring element $B$, denoted $A \cdot B$, is defined as:

In this formula:

1. $A \oplus B$: Dilate $A$ by $B$, expanding the object and filling in narrow gaps.
2. $(A \oplus B) \ominus B$: Erode the dilated result to refine and restore the main object boundary.

This approach fills in small gaps or holes, while retaining the essential structure of the object.

Geometric Interpretation of Closing

To understand closing, imagine rolling the structuring element $B$ around the outside boundary of $A$. The new boundary of $A \cdot B$ is formed by points that the structuring element reaches when rolled on the outside. This “rolling” fills gaps and small holes, and connects nearby components.

For instance, if an object in the image has a small internal gap, closing with a disk-shaped structuring element larger than the gap will fill it in, resulting in a smoother, more continuous object.

Example of Closing in Binary Images

Consider a binary image with a narrow gap:

Binary Image $A$:

Using a 2×2 square structuring element $B$:

Applying dilation to $A$ with $B$ will fill the gap in the center. Then, erosion will remove the outer border introduced by the dilation, restoring the main body of the object with the gap filled.

Properties of Closing

Closing has similar properties to opening:

1. Superset Property: $A \subseteq A \cdot B$
   • The closing of a set by a structuring element will always contain the original set.
2. Idempotence: $(A \cdot B) \cdot B = A \cdot B$
   • Similar to opening, applying closing multiple times with the same structuring element will yield the same result as applying it once.
3. Increasing Property: If $C \subseteq D$, then $C \cdot B \subseteq D \cdot B$
   • Closing preserves the subset relationship.

3. Duality of Opening and Closing

Opening and closing are dual operations, meaning that one can be defined in terms of the other using set complementation and reflection:

1. Duality of Opening:

   $$(A \circ B)^c = A^c \cdot B^N$$

2. Duality of Closing:

   $$(A \cdot B)^c = A^c \circ B^N$$

In these expressions:

• $A^c$ denotes the complement of set $A$.
• $B^N$ is the reflection of the structuring element $B$.

These dual relationships indicate that opening and closing are mirror images in how they handle set boundaries and structuring element fits.

4. Applications of Opening and Closing

The operations of opening and closing are widely used in image processing tasks, especially in preprocessing and segmentation, due to their ability to refine and adjust image features:

• Noise Reduction: Opening removes small objects or noise, while closing fills small gaps within objects, improving image clarity.
• Shape Smoothing: Both operations smooth object contours, but opening removes protrusions, and closing fills indentations.
• Object Separation and Connection: Opening can separate connected components, while closing connects nearby parts of an object.
• Boundary Simplification: By selectively removing small features, these operations simplify the boundary of objects for more efficient analysis.

The Hit-or-Miss Transformation is a fundamental morphological operation used in binary image processing. It is a pattern-matching technique that helps in detecting specific shapes or patterns within an image. This transformation is powerful in tasks where we need to locate distinct structural elements, such as corners, edges, or other predefined patterns.

1. Definition of the Hit-or-Miss Transformation

The Hit-or-Miss Transformation is used to locate specific configurations of pixels in a binary image by employing two structuring elements:

• A foreground structuring element $B_1$, which is designed to match pixels within the object or the target pattern.
• A background structuring element $B_2$, which defines the surrounding pixels or the pattern’s background.

Let $A$ represent the binary image, and $B_1$ and $B_2$ be the two structuring elements. The Hit-or-Miss Transformation of $A$ using $B_1$ and $B_2$ is defined as:

where:

• $A \ominus B_1$: Erosion of the image $A$ by the structuring element $B_1$.
• $A^c$: Complement of $A$, where the white (foreground) pixels become black (background) and vice versa.
• $A^c \ominus B_2$: Erosion of the complement of $A$ by $B_2$.
• $\cap$: Intersection of the two eroded images, giving the final output.

The transformation produces an output image where pixels match the pattern defined by $B_1$ within $A$ and the surrounding region matches the pattern defined by $B_2$. In simpler terms, it “hits” when both $B_1$ and $B_2$ match the image $A$ and “misses” otherwise.

2. Interpretation of the Hit-or-Miss Transformation

The Hit-or-Miss Transformation checks for exact configurations in an image. For example, if we want to locate a specific object or shape within an image, we define the shape as $B_1$ and the surroundings as $B_2$. This transformation is sensitive to the exact structure, as both $B_1$ and $B_2$ must match the configuration of $A$ precisely for a positive result.

This operation is particularly useful in detecting corner points, isolated pixels, or unique shapes that follow a strict pattern.

3. Example of the Hit-or-Miss Transformation

Let’s go through a practical example using a binary image and structuring elements.

Binary Image $A$:

Consider a binary image $A$ represented by the matrix below, where 1 represents foreground (white pixels) and 0 represents background (black pixels):

Structuring Elements $B_1$ and $B_2$:

Let’s define $B_1$ and $B_2$ to search for a particular pattern in $A$.

• Foreground Structuring Element $B_1$: This structuring element targets the central pixel and its immediate neighbors to the left and right.

• Background Structuring Element $B_2$: This structuring element looks for background pixels around the target area of $B_1$.

Applying the Hit-or-Miss Transformation

1. Step 1: Erode $A$ by $B_1$:

   • The result will include only those pixels in $A$ that exactly match the pattern of $B_1$.

2. Step 2: Complement $A$ and Erode by $B_2$:

   • Take the complement of $A$, making every 1 in $A$ a 0 and vice versa. Then erode this complemented image by $B_2$ to get areas where the background matches $B_2$.

3. Step 3: Intersect the Results:

   • The final result is the intersection of the two eroded images from steps 1 and 2. The resulting image will contain pixels that match both $B_1$ and $B_2$ in their respective foreground and background configurations.

4. Applications of the Hit-or-Miss Transformation

The Hit-or-Miss Transformation is particularly useful in applications requiring precise shape detection. Some examples include:

• Corner Detection: By choosing specific configurations for $B_1$ and $B_2$, the transformation can detect corners or junction points within an image.
• Shape Recognition: In industrial inspection and quality control, the Hit-or-Miss Transformation can be used to detect specific shapes or configurations within manufactured parts.
• Skeletonization: This transformation can help identify skeletal points or significant structural points within objects by sequentially identifying pixels that fit certain predefined patterns.

5. Properties of the Hit-or-Miss Transformation

The Hit-or-Miss Transformation has some key properties that influence its behavior in image processing tasks:

1. Translation Invariance: The transformation does not change if the image is translated (shifted) within the frame, as long as $B_1$ and $B_2$ are applied consistently.
2. Exact Matching Requirement: Both structuring elements $B_1$ and $B_2$ need to match exactly for a “hit” to be recorded, making the transformation sensitive to slight changes in the target pattern.
3. Duality: The transformation is self-dual; applying it to the complement of $A$ with the reflected structuring elements yields the same result.

Morphological image processing involves various algorithms that manipulate the structures within an image. These algorithms are based on the shape or morphology of the objects within the image and are particularly effective in binary and grayscale image processing.

1. Boundary Extraction

Boundary Extraction is a process used to identify the edges or contours of objects within an image. The boundary of an object can be extracted using morphological operations such as Erosion and Dilation.

Mathematical Definition:

Given a binary image $A$ and a structuring element $B$, the boundary $B_A$ can be extracted using the following formula:

where $A \ominus B$ represents the erosion of $A$ by $B$.

Example:

For a binary image $A$:

Assuming a square structuring element $B$:

1. Erode $A$ with $B$:

2. Subtract the eroded image from $A$:

Thus, the boundary of the object is highlighted.

2. Hole Filling

Hole Filling is used to fill small holes or gaps within an object in a binary image.

Mathematical Definition:

Given a binary image $A$, the filled image $F$ can be computed as:

where $\text{Fill}(A)$ fills all holes in $A$.

Example:

For a binary image $A$:

The holes can be filled by applying morphological operations such as dilation followed by erosion. The result is:

3. Extraction of Connected Components

This algorithm identifies and labels the connected components in a binary image.

Mathematical Definition:

The connected components can be defined using connectivity criteria. A common method is:

1. Labeling: Assign a label to each pixel in the image.
2. Connectedness: Two pixels are connected if they are adjacent in the neighborhood defined by a structuring element.

Example:

For a binary image $A$:

The connected components can be extracted and labeled as follows:

1. Label first component (1):

The output $A’$ shows the labeled connected components.

4. Convex Hull

The Convex Hull of a set of points in the image is the smallest convex shape that can enclose all the points.

Mathematical Definition:

The convex hull $\text{CH}(A)$ can be defined as:

where $a_i$ are the points in $A$.

Example:

Given a set of points representing a binary shape in an image:

The convex hull would result in a shape that minimally encloses all points, illustrated as:

5. Thinning

Thinning reduces objects in a binary image to their skeletal form, often used for shape representation.

Mathematical Definition:

Thinning can be iteratively defined as removing pixels from the object without changing its topology.

Example:

For a binary image $A$:

After applying a thinning algorithm, we might get:

6. Thickening

Thickening is the inverse of thinning and is used to expand the object in the binary image.

Mathematical Definition:

Thickening can be defined as applying dilation iteratively to enhance the shape of the object.

Example:

Using the previous $A$:

7. Skeletons

The Skeleton of an object is a representation that captures the object’s structure while preserving its topology.

Mathematical Definition:

Skeletonization can be performed by iteratively applying thinning until no further reduction is possible.

Example:

From a binary shape $A$:

The skeleton representation would be:

8. Pruning

Pruning is a process used to remove branches from the skeleton that are not significant in the overall structure.

Mathematical Definition:

Pruning is performed by analyzing the branches of the skeleton and removing those below a certain length or importance.

Example:

For a skeleton $S$:

If a branch is less than a specific length, it may be removed:

9. Morphological Reconstruction

Morphological Reconstruction is an operation used to recover shapes in a binary image from a marker image.

Mathematical Definition:

The reconstruction $R$ can be defined as:

where $A$ is the mask, and $B$ is the marker.

Example:

Let $A$ represent a binary image and $B$ a marker:

The reconstruction process will yield an output where the shape in $B$ is preserved within the constraints of $A$.

Gray-scale morphology is a powerful image processing technique used in computer vision and image analysis. It involves mathematical operations on gray-scale images that allow for the manipulation and extraction of image structures. Unlike binary morphology, which works on binary images (images with only two levels of intensity), gray-scale morphology operates on images with varying intensities, making it suitable for tasks where information is contained in shades or gradients.

Basic Concepts of Gray-Scale Morphology

Gray-scale morphology relies on mathematical concepts like set theory and min-max operations. The two primary operations in gray-scale morphology are erosion and dilation, which form the foundation for other morphological operations like opening, closing, and morphological reconstruction.

1. Erosion and Dilation

1.1 Erosion

Gray-scale erosion reduces the brightness of the bright parts in an image, which can remove small bright details. It involves “shrinking” objects in an image, making it useful for tasks like removing noise or separating connected objects.

For a given gray-scale image $f(x, y)$ and a structuring element $b(x, y)$, gray-scale erosion is defined as:

where:

• $f(x, y)$: Gray-scale input image.
• $b(x, y)$: Structuring element.
• $(s, t) \in B$: Set of coordinates in the structuring element.

Example of Erosion:

Consider a 3×3 structuring element of ones:

Applying erosion will reduce the bright regions (local maxima) in the original image, which helps in background elimination or noise reduction.

1.2 Dilation

Gray-scale dilation, on the other hand, brightens the brighter parts, enhancing them and “expanding” objects in the image. This is useful for filling gaps and enhancing details.

The gray-scale dilation of $f(x, y)$ by a structuring element $b(x, y)$ is defined as:

Example of Dilation:

Using the same structuring element $b$ as above, applying dilation will intensify bright spots or enhance edges in the image.

2. Opening and Closing

Building upon erosion and dilation, we define two composite operations, opening and closing.

2.1 Opening

Gray-scale opening is the process of applying erosion followed by dilation. It smooths contours, breaks narrow connections, and removes small bright areas.

Opening of $f(x, y)$ with structuring element $b(x, y)$ is given by:

Example of Opening:

Applying opening on an image with noise and small bright regions will remove these regions, leaving only the main object structures.

2.2 Closing

Gray-scale closing is dilation followed by erosion, which fills gaps and connects small, close objects.

Closing of $f(x, y)$ with structuring element $b(x, y)$ is given by:

Example of Closing:

When an image has small dark regions or holes, applying closing will fill these areas, making the object boundaries smoother.

3. Some Basic Gray-Scale Morphological Algorithms

Several algorithms are built on basic operations to perform more complex image analysis tasks:

3.1 Top-Hat Transform

The top-hat transform is useful for highlighting bright areas on a darker background. It is defined as the difference between the original image and its opening:

This transform enhances small, bright features within the image, making them stand out.

3.2 Bottom-Hat Transform

The bottom-hat transform is the difference between the closing of an image and the original image:

This transform highlights small, dark features in the image.

4. Gray-Scale Morphological Reconstruction

Morphological reconstruction is a technique to modify images based on a reference, or “marker,” image. It refines shapes while preserving essential structures, making it useful for segmenting images.

4.1 Reconstruction by Dilation

Gray-scale reconstruction by dilation starts with a marker image $g$, which is iteratively dilated under the constraint of the original image $f$, known as the mask:

where $g \leq f$ initially.

Example of Reconstruction by Dilation:

Suppose $g$ highlights specific areas in $f$. Reconstruction by dilation will enhance these regions, expanding them while respecting the boundaries of $f$.

4.2 Reconstruction by Erosion

This is often used for contrast enhancement, background elimination, and shape recovery by iteratively applying erosion under the mask $f$.