Digital image processing is a discipline that applies mathematical and computational techniques to the representation, enhancement, analysis, and reconstruction of images. Its applications span various fields, including medical imaging, remote sensing, computer vision, and photography. This note delves into the fundamental mathematical tools and concepts that underpin digital image processing, offering insights into how these tools enable the manipulation and analysis of digital images.
Arrays in Image Processing
Definition:
In image processing, an image is represented as a two-dimensional array, where each element corresponds to the intensity value of a pixel. Mathematically, we can denote an image as an array , where represents the row index, represents the column index, and represents the intensity value of the pixel at position .
Operations:
Element-wise Operations:
- Arrays facilitate element-wise operations, where mathematical operations are applied individually to each pixel in the image array.
- Example: Increasing the brightness of an image using array addition:
Let be the original image array, and let be a constant representing the amount of brightness adjustment. The brightness-adjusted image can be obtained as:
for all .
Broadcasting:
- Broadcasting allows arrays of different shapes to be combined in element-wise operations, enabling efficient manipulation of images with scalar values or arrays of different sizes.
- Example: Broadcasting in array subtraction to create a negative image:
Let be the original image array, and let be a matrix representing the maximum intensity value. The negative image can be obtained as:
for all .
Matrices in Image Processing
Definition:
Matrices in image processing are used to represent transformations and filters applied to images. A matrix operation involves applying a mathematical operation to each pixel or a group of pixels in the image.
Operations:
Matrix Convolution:
- Convolution involves sliding a kernel (matrix) over an image and performing element-wise multiplication followed by summation to generate a new pixel value.
- Example: Applying a Gaussian blur filter using matrix convolution:
Let be the original image array, and let be the Gaussian blur kernel matrix. The blurred image can be obtained by convolving the image array with the kernel matrix using the convolution operation.
where is the size of the kernel.
Matrix Transformation:
- Matrices are used to represent geometric transformations such as rotation, scaling, and translation applied to images.
- Example: Rotating an image using matrix transformation:
Let be the original image array, and let be the transformation matrix representing the rotation operation. The rotated image can be obtained by applying the matrix transformation to the coordinates of each pixel in the original image array .
where are the coordinates of the pixel in the rotated image obtained by applying the transformation matrix to the coordinates of the corresponding pixel in the original image.
Linear Operations
Definition:
A linear operation is one that satisfies two properties: additivity and homogeneity. Additivity implies that the operation behaves the same way regardless of whether it is applied separately or collectively to multiple inputs. Homogeneity dictates that scaling the input by a constant results in scaling the output by the same constant.
Mathematical Concepts:
Let be an input image and be the output image obtained after applying a linear operation to . Mathematically, a linear operation can be represented as:
where is a linear combination of the input pixels:
where and are constants.
Example:
A common example of a linear operation in image processing is contrast adjustment using histogram equalization. Here, the operation adjusts the contrast of an image by redistributing pixel intensities in a linear manner across the entire dynamic range.
Nonlinear Operations
Definition:
A nonlinear operation is one that does not satisfy the properties of additivity and homogeneity. Nonlinear operations can alter the relationship between input and output, resulting in complex transformations of pixel values.
Mathematical Concepts:
Let be an input image and be the output image obtained after applying a nonlinear operation to . Mathematically, a nonlinear operation can be represented as:
where is a function of the input pixels that cannot be expressed as a linear combination.
Example:
A typical example of a nonlinear operation is image thresholding, where pixels are classified as either foreground or background based on a specified threshold value. The transformation is nonlinear as it abruptly changes the pixel values based on a threshold, without considering their relationship to neighboring pixels.
Comparison
Linear Operations:
- Maintain additivity and homogeneity properties.
- Preserve relationships between pixel values.
- Examples include contrast adjustment, scaling, and translation.
Nonlinear Operations:
- Do not satisfy additivity and homogeneity properties.
- Introduce complex transformations to pixel values.
- Examples include thresholding, edge detection, and nonlinear filtering.
Arithmetic Operations
Arithmetic operations involve mathematical manipulations of pixel values in digital images. These operations can be performed on individual pixels or groups of pixels to achieve specific effects such as contrast adjustment, brightness modification, and blending of images.
Mathematical Concepts:
Addition:
Addition involves adding a constant value to each pixel in an image or combining corresponding pixels from multiple images.
where is the output pixel value, is the input pixel value, and is a constant.
Subtraction:
Subtraction subtracts a constant value from each pixel in an image or computes the difference between corresponding pixels of two images.
Multiplication:
Multiplication scales the intensity values of pixels by a constant factor.
Division:
Division divides the intensity values of pixels by a constant factor.
Blending:
Blending combines two images by weighting their pixel values.
where is the blending factor, and and are the input images.
Applications:
Contrast Adjustment:
Arithmetic operations such as addition and multiplication are used to adjust the contrast of images, enhancing their visual appearance.
Brightness Modification:
Addition and subtraction operations are employed to modify the brightness of images, making them lighter or darker.
Image Blending:
Blending operations combine multiple images to create composite images or transition effects.
Noise Reduction:
Multiplication and division operations are utilized to reduce noise in images by smoothing pixel values.
Image Arithmetic:
Arithmetic operations are applied to perform pixel-wise arithmetic between two or more images, enabling operations like addition, subtraction, multiplication, and division.
Example:
Brightness Adjustment:
pythonimport cv2
# Load image
image = cv2.imread('image.jpg')
# Increase brightness by adding a constant value
brightened_image = cv2.add(image, 50)
# Display original and brightened images
cv2.imshow('Original Image', image)
cv2.imshow('Brightened Image', brightened_image)
cv2.waitKey(0)
cv2.destroyAllWindows()
Set and Logical Operations
Set and Logical Operations in Image Processing
In the realm of image processing, set and logical operations play a pivotal role, especially when dealing with binary images. These images are characterized by pixels that have one of two possible values: 0 or 1, representing black or white, respectively. Such operations are fundamental for executing tasks like image segmentation, object detection, and morphology. Grasping the mathematical concepts and applications of these operations is crucial for the effective manipulation of digital images.
Set Operations
Union: The union of two images (sets) A and B encompasses all pixels that belong to at least one of the images. Mathematically, it’s expressed as:
For binary images, the union operation can be implemented pixel-wise using the logical OR operation.
Intersection: The intersection of two images A and B includes only those pixels that are present in both A and B. Formally, it is defined as:
This operation can be executed on a pixel-wise basis in binary images using the logical AND operation.
Difference: The difference between two images A and B (denoted as ) consists of pixels that are in A but not in B. It’s defined as:
For binary images, this can be achieved through a combination of logical operations.
Complement: The complement of an image A includes all pixels not in A. In the context of binary images, the complement is obtained by inverting 0s to 1s and vice versa.
Logical Operations
NOT: The NOT operation inverts the value of each pixel in a binary image, turning 1s into 0s and vice versa.
AND: The AND operation between two images A and B sets a pixel to 1 if the corresponding pixel is 1 in both images, otherwise, it is set to 0.
OR: The OR operation sets a pixel to 1 if the corresponding pixel is 1 in either image A or B (or both).
XOR: The XOR (exclusive OR) operation sets a pixel to 1 only if the corresponding pixel is 1 in one and only one of the two images.
Applications:
- Image Segmentation: Logical operations are extensively used to isolate specific regions within an image, aiding in segmentation.
- Object Detection: Set operations facilitate the identification and extraction of objects within images.
- Morphological Operations: Many morphological transformations, crucial for shape analysis, are based on set operations.
Example:
For instance, to extract a specific object from an image, assume represents the original image and is a mask where the object of interest is marked with 1s (and the background with 0s). The object can be isolated using the intersection operation:
This operation effectively segments the object from the background by zeroing out all pixels not belonging to the object.
Set and logical operations are indispensable in image processing, enabling a broad spectrum of image manipulations through straightforward mathematical operations. From segmenting images and detecting objects to conducting morphological analyses, these operations are foundational to developing robust image processing techniques.
Logical operations
Logical Operations in Image Processing
Logical operations, fundamental to image processing, are utilized extensively in manipulating binary images. Binary images consist of pixels that are assigned one of two possible values: 0 or 1. These operations enable tasks such as image enhancement, segmentation, and feature extraction by applying logical functions to the pixel values. Understanding these operations requires a grasp of the mathematical concepts behind them, alongside practical examples to illustrate their application.
Logical NOT
The Logical NOT operation, or complement, inverts each pixel value in an image. If the original pixel value is 1 (white), it becomes 0 (black), and vice versa.
Mathematically, for a pixel value , the NOT operation is defined as:
Example: If a binary image pixel , applying NOT results in .
Logical AND
The Logical AND operation compares corresponding pixels from two images and assigns a value of 1 to the output pixel only if both input pixels are 1. If either or both pixels are 0, the output pixel is set to 0.
Mathematically, for corresponding pixel values and from two images, the AND operation is defined as:
Example: If and , then . If either or (or both), the result is 0.
Logical OR
The Logical OR operation compares corresponding pixels from two images and assigns a value of 1 to the output pixel if at least one of the input pixels is 1. The output pixel is set to 0 only if both input pixels are 0.
Mathematically, for corresponding pixel values and , the OR operation is defined as:
This ensures the output is 1 if either or is 1, considering binary images where pixel values are either 0 or 1.
Example: If and , then .
Logical XOR
The Logical XOR (exclusive OR) operation assigns a value of 1 to the output pixel if and only if the input pixels have different values. If both input pixels are the same, the output pixel is set to 0.
Mathematically, for pixel values and , the XOR operation is defined as:
This formula ensures that the output is 1 only if and are different.
Example: If and , then . If , the result is 0.
Applications in Image Processing
Logical operations are instrumental in a variety of image processing tasks, including:
- Image Enhancement: Adjusting the contrast or brightness of an image.
- Image Segmentation: Isolating specific components from the rest of the image, such as separating foreground from background.
- Feature Extraction: Identifying and isolating specific features within images, which is crucial for pattern recognition and image classification tasks.
- Noise Reduction: Removing unwanted artifacts from images to improve their quality.
Practical Example
Consider two binary images and , where you want to highlight the differences between them. You could use the XOR operation to create a new image that showcases these differences:
For every pixel position in images and :
- If , then (no difference).
- If , then (highlighting a difference).
This operation effectively emphasizes the changes or discrepancies between the two images, which can be particularly useful in applications like motion detection or image comparison.
Fuzzy sets
Introduction to Fuzzy Sets in Image Processing
Fuzzy set theory in image processing allows for the representation of image elements with degrees of belonging, rather than binary classifications. This is particularly useful for dealing with the inherent ambiguities and nuances in images.
Mathematical Basis of Fuzzy Sets
- Fuzzy Set Definition: A fuzzy set in a universe of discourse is defined by a membership function which maps each element in to a real number in the interval . The value of represents the degree of membership of in the fuzzy set , with 1 indicating full membership, 0 indicating no membership, and values in between indicating partial membership.
Fuzzy Set Operations
Fuzzy set operations extend conventional set operations to accommodate the concept of partial membership. These operations include:
- Union: The union of two fuzzy sets and is a fuzzy set with a membership function for all in .
- Intersection: The intersection of two fuzzy sets and is a fuzzy set with a membership function for all in .
- Complement: The complement of a fuzzy set is a fuzzy set with a membership function for all in .
Application in Image Processing
Fuzzy set theory is applied in various image processing tasks, such as segmentation, noise reduction, and edge detection, enabling these tasks to handle ambiguity and partial truths efficiently.
Example: Fuzzy Logic for Image Segmentation
Let’s consider a practical example to illustrate the application of fuzzy sets in image segmentation:
- Objective: Segment an image into foreground and background based on pixel intensity.
- Approach: Define a fuzzy set “Foreground” with a membership function that reflects the degree to which each pixel belongs to the foreground based on its intensity.
Suppose the intensity of a pixel ranges from 0 (black) to 255 (white). A simple membership function for the “Foreground” could be:
This function implies that a pixel with intensity 0 (black) has 0 membership in the Foreground (fully in the background), and a pixel with intensity 255 (white) has 1 membership (fully in the foreground). A pixel with an intensity of 127.5 would have a membership value of 0.5, indicating it is equally part of the foreground and background.
Processing:
- Apply the Membership Function: For each pixel, calculate its membership value in the “Foreground” set.
- Classification: Pixels can be classified based on their membership values. For instance, a threshold might be used to decide if a pixel is more foreground than background.
- Post-Processing: Further refine the segmentation with morphological operations or additional fuzzy logic rules to enhance the segmentation quality.
Fuzzy sets introduce flexibility and nuance into image processing, allowing for the effective handling of the ambiguity present in real-world images. Through the use of membership functions and fuzzy operations, images can be processed in a way that mirrors human logic and perception more closely than binary approaches, facilitating advanced applications and improving outcomes in tasks such as image segmentation, noise reduction, and edge detection.
Spatial Operations
Spatial operations in image processing are fundamental techniques that manipulate pixels in an image based on their spatial configuration and relationships. These operations play a crucial role in various image processing tasks, including filtering, edge detection, image enhancement, and more. Understanding the mathematical concepts behind spatial operations is essential for anyone working in digital image processing.
Introduction to Spatial Operations
Spatial operations can be broadly categorized into two types: point operations and neighborhood operations. Point operations, also known as pixel-wise operations, modify the value of each pixel independently of its neighbors. Neighborhood operations, on the other hand, take into account a pixel and its surrounding neighbors, applying transformations based on this contextual information.
Point Operations
Point operations are straightforward: each pixel in an image is transformed independently according to a specific function. Mathematically, this is represented as:
Here, is the original pixel value at coordinates , is the transformed pixel value, and is the transformation function that is applied to the pixel.
Example: Image Negatives
For instance, to create an image negative, the transformation function would be:
where is the maximum possible pixel intensity value. For an 8-bit image, would be 256, meaning that this operation inverts the colors of the image.
Neighborhood Operations
Neighborhood operations consider a pixel and its immediate neighbors, where the output pixel value is determined based on the pixel values within a defined neighborhood around it. These operations often use kernels or masks, small matrices that are applied to each pixel and its neighbors.
The mathematical representation of a neighborhood operation is:
In this equation, represents the weight assigned to a neighbor at offset within the neighborhood defined by a kernel, and and define the kernel’s size.
Example: Smoothing Filter
A simple example of a neighborhood operation is a smoothing filter, which reduces noise in an image. Using a mean filter, where all weights in the kernel are equal, and for a 3×3 kernel, the weights for all , leading to:
This operation calculates the average of the pixel values in the 3×3 neighborhood around each pixel, effectively smoothing the image.
Edge Detection as a Spatial Operation
Edge detection highlights significant changes in pixel intensity, corresponding to edges within the image, and is a pivotal application of neighborhood operations. The Sobel operator, for instance, uses two 3×3 kernels designed to detect horizontal and vertical changes in intensity, respectively.
Sobel Operator
The Sobel operator uses for horizontal and for vertical changes, defined as follows:
The edge strength, or gradient magnitude, is then calculated using:
Spatial operations are indispensable in image processing, offering a wide range of techniques for pixel manipulation. From adjusting individual pixel intensities to considering the broader context of a pixel’s neighborhood, these operations facilitate advanced image processing tasks such as enhancement, noise reduction, and edge detection. A solid grasp of the mathematical principles underlying spatial operations is vital for developing effective algorithms and applications in image processing.
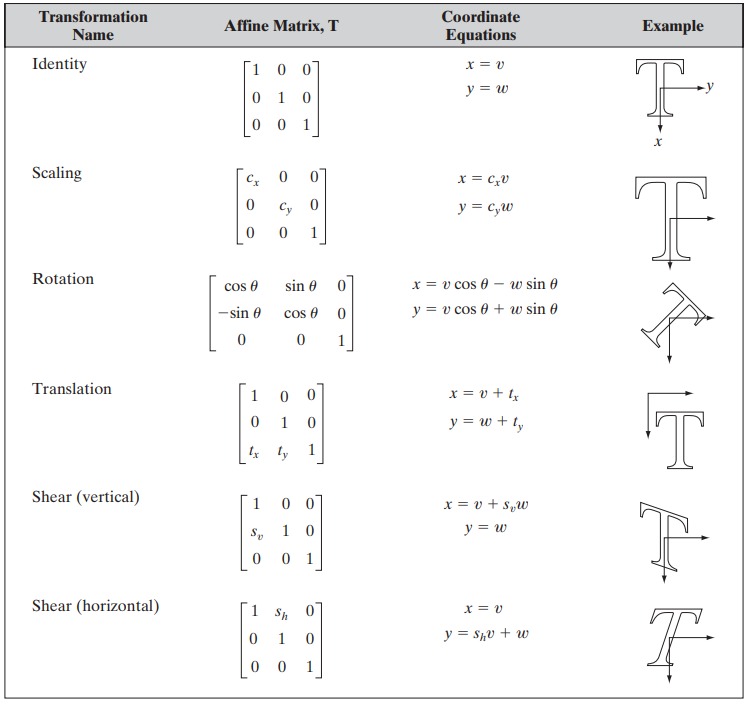
Vector and Matrix Operations
Vectors and matrices are fundamental mathematical structures used extensively in various fields including mathematics, physics, computer science, and engineering. Vector operations deal with manipulating arrays of numbers, while matrix operations extend these concepts to two-dimensional arrays.
Vector Operations
Vector Addition: Addition of two vectors involves adding corresponding elements together.
- Example:
- Example:
Vector Subtraction: Subtraction of two vectors involves subtracting corresponding elements.
- Example:
- Example:
Scalar Multiplication: Multiplying a vector by a scalar involves multiplying each element of the vector by that scalar.
- Example:
- Example:
Dot Product (Scalar Product): The dot product of two vectors yields a scalar.
- Example:
- Example:
Matrix Operations
Matrix Addition: Addition of two matrices involves adding corresponding elements.
- Example:
- Example:
Matrix Subtraction: Subtraction of two matrices involves subtracting corresponding elements.
- Example:
- Example:
Scalar Multiplication: Multiplying a matrix by a scalar involves multiplying each element of the matrix by that scalar.
- Example:
- Example:
Matrix Multiplication: Multiplication of matrices involves multiplying rows of the first matrix by columns of the second.
- Example:
- Example:
Code Example (Python using NumPy)
pythonimport numpy as np
# Vector Operations
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
# Addition
c = a + b
print("Vector Addition:", c)
# Subtraction
d = a - b
print("Vector Subtraction:", d)
# Scalar Multiplication
alpha = 2
e = alpha * a
print("Scalar Multiplication:", e)
# Dot Product
dot_product = np.dot(a, b)
print("Dot Product:", dot_product)
# Matrix Operations
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
# Addition
C = A + B
print("Matrix Addition:", C)
# Subtraction
D = A - B
print("Matrix Subtraction:", D)
# Scalar Multiplication
beta = 3
E = beta * A
print("Scalar Multiplication:", E)
# Matrix Multiplication
F = np.dot(A, B)
print("Matrix Multiplication:", F)
Understanding vector and matrix operations is crucial in various computational and mathematical tasks. These operations form the backbone of many algorithms and mathematical models, making them essential concepts to grasp in fields ranging from machine learning to physics. By mastering these operations, one can efficiently manipulate and analyze multidimensional data structures.
Image Transforms
Image transforms are essential tools in image processing, computer vision, and graphics, allowing the conversion of images from one domain to another to highlight certain features or facilitate various operations. Here’s a detailed look at some of the most critical mathematical concepts and transforms in this area.
Fourier Transform
Overview: The Fourier Transform decomposes an image into its sine and cosine components, effectively transforming it from the spatial domain to the frequency domain.
Mathematical Concept: For a continuous 2D function , the Fourier Transform is defined as: where is the transform result, represent spatial frequencies, and is the square root of -1.
Applications:
- Image filtering
- Image compression
- Feature extraction
Inverse Fourier Transform
Overview: This process reverses the Fourier Transform, converting data from the frequency domain back to the spatial domain.
Mathematical Concept:
Applications:
- Reconstructing images post frequency domain filtering
- Analysis of frequency domain modifications
Discrete Fourier Transform (DFT)
Overview: The digital variant of the Fourier Transform, used for analyzing digital images by converting them into frequency components.
Mathematical Concept:
Applications:
- Digital image processing
- Employing Fast Fourier Transform (FFT) for quick computations
Cosine Transform (DCT)
Overview: The Discrete Cosine Transform is a variant that uses cosine functions, well-suited to images for its efficiency in handling real data.
Mathematical Concept:
Applications:
- JPEG image compression
- Signal processing
Haar Transform
Overview: A simple wavelet transform using square-shaped functions for data representation, focusing on differences and averages.
Mathematical Concept: It calculates based on piecewise constant functions (Haar functions), simplifying the image into a series of averages and differences.
Applications:
- Image compression
- Feature detection
Wavelet Transforms
Overview: These transforms decompose an image into wavelets, providing both frequency and spatial information effectively.
Mathematical Concept: where is the mother wavelet, and and are the scaling and translation parameters, respectively.
Applications:
- Image compression (e.g., JPEG 2000)
- Image denoising
Understanding the mathematical principles behind image transforms is vital for developing algorithms for image processing tasks like compression, enhancement, and feature extraction. Each transform has its unique advantages and applications, highlighting the importance of selecting the appropriate method for specific tasks.
Probabilistic Methods
Probabilistic methods in image processing involve using statistical models to represent the uncertainty and variability present in image data. These methods provide powerful tools for image analysis, enhancement, restoration, segmentation, and recognition by modeling the stochastic nature of image generation and acquisition processes. Below, we delve into some fundamental concepts and their mathematical underpinnings.
Bayesian Framework
Overview: The Bayesian framework provides a systematic approach for incorporating prior knowledge along with observed data to make inferences about images. It is particularly useful in image restoration and reconstruction tasks.
Mathematical Concept: The Bayesian theorem is given by: where:
- is the posterior probability of the model parameters given the observed data .
- is the likelihood of observing given .
- is the prior probability of , representing our knowledge about before observing .
- is the evidence or marginal likelihood of , often acting as a normalizing constant.
Applications:
- Image deblurring
- Image denoising
- Super-resolution
Markov Random Fields (MRFs)
Overview: MRFs are used to model spatial dependencies in image pixels, representing the image as a stochastic process. They are extensively used in image segmentation and texture analysis.
Mathematical Concept: An MRF is defined over a graph , where represents vertices or pixels, and represents edges connecting neighboring pixels. The probability of a configuration given an MRF is: where:
- is the set of cliques in the graph.
- is a potential function that assigns a real value to the configuration of pixels in clique .
- is the partition function that ensures the probabilities sum up to 1.
Applications:
- Image segmentation
- Texture recognition
Gaussian Mixture Models (GMMs)
Overview: GMMs are used to model the distribution of pixel intensities or feature vectors in an image. They are particularly useful in modeling complex distributions for tasks like image segmentation and clustering.
Mathematical Concept: A GMM is a weighted sum of Gaussian distributions, given by: where:
- is the data point (e.g., pixel intensity).
- represents the parameters of the model (, , ), where is the weight, is the mean, and is the covariance matrix of the th Gaussian.
- is the Gaussian distribution.
Applications:
- Image segmentation
- Background subtraction
Hidden Markov Models (HMMs)
Overview: HMMs model sequences of observable events generated by a sequence of internal states. They are used in image processing for tasks that can be represented as a sequence, such as contour detection and texture classification.
Mathematical Concept: An HMM is defined by:
- A set of states .
- Transition probabilities where represents the probability of transitioning from state to state .
- Emission probabilities where is the probability of observing symbol from state .
- Initial state probabilities .
The likelihood of observing a sequence given the model is:
Applications:
- Contour detection
- Texture classification
Expectation-Maximization (EM) Algorithm
Overview: The EM algorithm is a method used to find maximum likelihood estimates of parameters in probabilistic models, particularly when the model involves latent variables. It is widely used with GMMs and HMMs.
Mathematical Concept: The EM algorithm iterates between two steps:
- Expectation step (E-step): Calculate the expected value of the log likelihood function, with respect to the conditional distribution of the latent variables given the observed data and current estimate of the model parameters.
- Maximization step (M-step): Maximize the expected log likelihood found in the E-step to obtain a new estimate of the parameters.
Applications:
- Parameter estimation for GMMs and HMMs
- Image reconstruction
Probabilistic methods in image processing leverage statistical models to deal with uncertainties and variabilities in images. From incorporating prior knowledge and modeling spatial dependencies to handling complex distributions and sequences, these methods underpin a wide range of applications, significantly enhancing our ability to process and analyze images in various domains.
