A color model, also called a color space or color system, is designed to provide a standardized method for specifying colors. This is essential for ensuring consistency and accuracy across various platforms and applications. In essence, a color model defines a coordinate system and a subspace within that system, where a unique point represents each color. The importance of color models lies in their ability to make color specification universal so that colors can be communicated and reproduced across different devices and mediums without ambiguity.
Most modern color models are developed with specific purposes in mind. Some are oriented toward hardware, such as monitors and printers, while others are tailored for applications where color manipulation is the primary goal, like in digital graphics and animation. For example, in digital image processing, some of the most widely used hardware-oriented models are the RGB (red, green, blue) model, which is essential for color monitors and a range of video cameras. Similarly, the CMY (cyan, magenta, yellow) and CMYK (cyan, magenta, yellow, black) models are integral to the color printing process.
Another significant color model is the HSI (hue, saturation, intensity) model, which closely mirrors how humans perceive and describe color. One of the key advantages of the HSI model is that it separates color information from grayscale data, allowing it to be particularly effective in image processing tasks that require grayscale manipulation. This decoupling of color and grayscale information makes the HSI model versatile and well-suited to a variety of image processing techniques that focus on grayscale.
Due to the broad scope of color science and its many applications, there are numerous color models in use today. Each model has been developed with specific goals, whether for hardware, software, or color theory research. While some of these models are interesting and informative in their own right, the focus of this discussion is on the leading models used in digital image processing. Once the fundamental concepts behind these models are understood, it becomes easier to grasp the workings of other color models in the broader field of color science.
The RGB Color Model
Understanding Safe RGB Colors: Mathematical Concepts
The 216 safe colors in the RGB color model are derived using specific RGB values that ensure consistent color reproduction across various systems and devices. These values are: 0, 51, 102, 153, 204, and 255. By constructing color combinations from these values, we get a total of possible colors. This color space ensures compatibility for displays that are limited in the number of colors they can render, making it ideal for web design and other digital applications.
Each color is represented by a triplet of these RGB values, and for convenience, the hexadecimal (hex) system is often used. Hexadecimal is a base-16 system where digits range from 0–9 and A–F (where A = 10, B = 11, …, F = 15). In this system, the RGB values are expressed in two-digit hexadecimal equivalents, ranging from 00 to FF. For example, black is represented as or hex 000000, and white is represented as or hex FFFFFF.
Using the hex system, a 24-bit RGB color consists of three 8-bit values (one for each primary color), allowing up to 16,777,216 possible color combinations. However, for safe web colors, only the 216 evenly spaced combinations are used. These colors form a subset of the full RGB color cube and are known to reproduce consistently on different systems.
The following table summarizes the key RGB values and their hex equivalents for the safe colors:
| RGB Decimal Value | Hexadecimal Equivalent |
|---|---|
| 0 | 00 |
| 51 | 33 |
| 102 | 66 |
| 153 | 99 |
| 204 | CC |
| 255 | FF |
Each safe color is formed by combining these RGB values in triplets. For example, the purest red is represented as , or hex FF0000, where the red channel is fully saturated, and both the green and blue channels are at their minimum values. Similarly, cyan is represented as , or hex 00FFFF.
Mathematical Representation of the RGB Cube
In the RGB model, colors are visualized within a three-dimensional cube. Each axis of this cube represents one of the primary colors (R, G, B). The coordinates of each point within this cube define a specific color. The unit cube’s vertices represent the primary colors, secondary colors (cyan, magenta, yellow), black, and white. The grayscale spectrum, where , lies along the diagonal from black to white. For instance, gray can be represented by any point where all three RGB values are equal, such as .
Safe Web Colors and Their Importance
Safe web colors, also known as system-safe colors, are crucial in ensuring consistent color reproduction across different devices and platforms. Many systems are limited to displaying 256 colors, and within this constraint, 216 colors are considered safe. These safe colors are chosen because they are consistently rendered across different operating systems, browsers, and display hardware. This standardization is particularly important for web developers who need to ensure that the colors they use appear the same for all viewers.
By using only these 216 colors, developers can avoid color distortions and ensure that their designs are seen as intended. Safe colors are especially critical for web design, where user experience can be affected by inconsistent color rendering.
The CMY and CMYK Color Models
In the world of color processing, the RGB (Red, Green, Blue) model is widely used for digital screens and devices, while the CMY and CMYK models are essential for print media. These models play a crucial role in how color is produced in printing processes, where light behaves differently compared to digital displays.
The CMY Model
The CMY color model stands for Cyan, Magenta, and Yellow, which are the secondary colors in the RGB model and the primary colors in pigment-based systems. When light hits a surface coated with cyan pigment, it absorbs red light and reflects the green and blue components. Similarly, magenta absorbs green light, and yellow absorbs blue light, leaving a mixture of the other two primary light components. This concept of subtractive color mixing is fundamental to printing because it starts with white light and subtracts components to produce colors.
In mathematical terms, the conversion from RGB to CMY is straightforward, as shown in the equation below:
This equation simply indicates that the cyan value is obtained by subtracting the red component from 1, magenta by subtracting the green component, and yellow by subtracting the blue component. The result is the CMY value, normalized to the range .
The Need for Black: Enter the CMYK Model
While the CMY model provides a good approximation for most colors, it has limitations when it comes to producing deep blacks. In theory, mixing equal amounts of cyan, magenta, and yellow should yield black, but in practice, this results in a muddy brownish-black color due to imperfections in pigment formulation.
To solve this problem, a fourth color, black (K for “key”), is added, giving us the CMYK model. The role of the black ink is to provide depth and definition, especially for text and dark areas in an image. This addition is critical in printing processes, as it reduces the amount of ink required for producing dark colors and enhances overall print quality.

Application in Printing
The CMYK color model is used extensively in four-color printing. When publishers or print designers talk about “four-color process printing,” they are referring to the use of cyan, magenta, yellow, and black inks to reproduce a wide range of colors. Each color is printed separately and layered onto the page to create the final image.
To illustrate the concept visually, imagine the RGB color cube (as shown in Figure 6.11 in the image), which represents the full range of colors visible on a digital screen. The CMY color model is its counterpart in printing. However, instead of emitting light, it relies on the absorption and reflection of light from the paper surface. The addition of black in the CMYK model fine-tunes this process, ensuring high-quality reproduction of printed colors.
The HSI Color Model
The process of transitioning between RGB and CMY color models is relatively straightforward and particularly well-suited for hardware implementations. RGB aligns with the human visual system, as our eyes are highly sensitive to red, green, and blue light. This makes the RGB model ideal for tasks like image capture or display, where color generation is crucial. However, while RGB excels at producing colors, it is less practical to describe them in human terms. We don’t typically refer to a color by specifying the percentage of red, green, and blue; instead, we think of colors in terms of hue, saturation, and brightness.
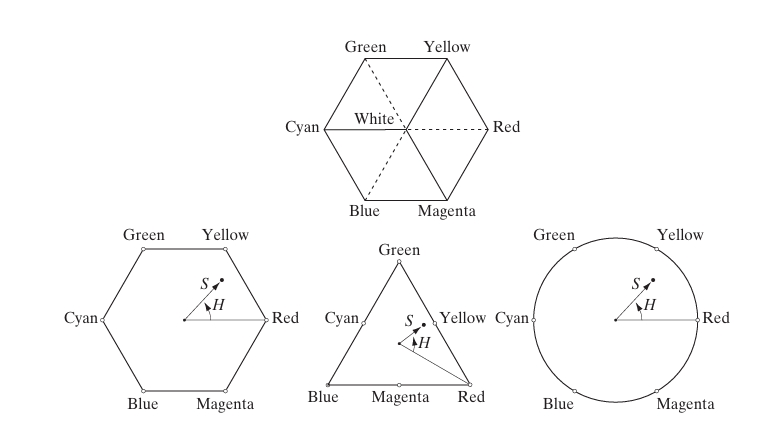
Hue, saturation, and brightness offer a more intuitive way for humans to interpret and describe colors. Hue refers to the type of color we perceive, such as red, blue, or yellow. Saturation measures how pure the color is, with highly saturated colors appearing vivid, while less saturated colors look diluted with white. Brightness, which can be more subjective, indicates how light or dark a color appears. These attributes form the foundation of the HSI (Hue, Saturation, Intensity) color model, which decouples the intensity component from the color information, making it more suitable for tasks that require human interpretation of colors.
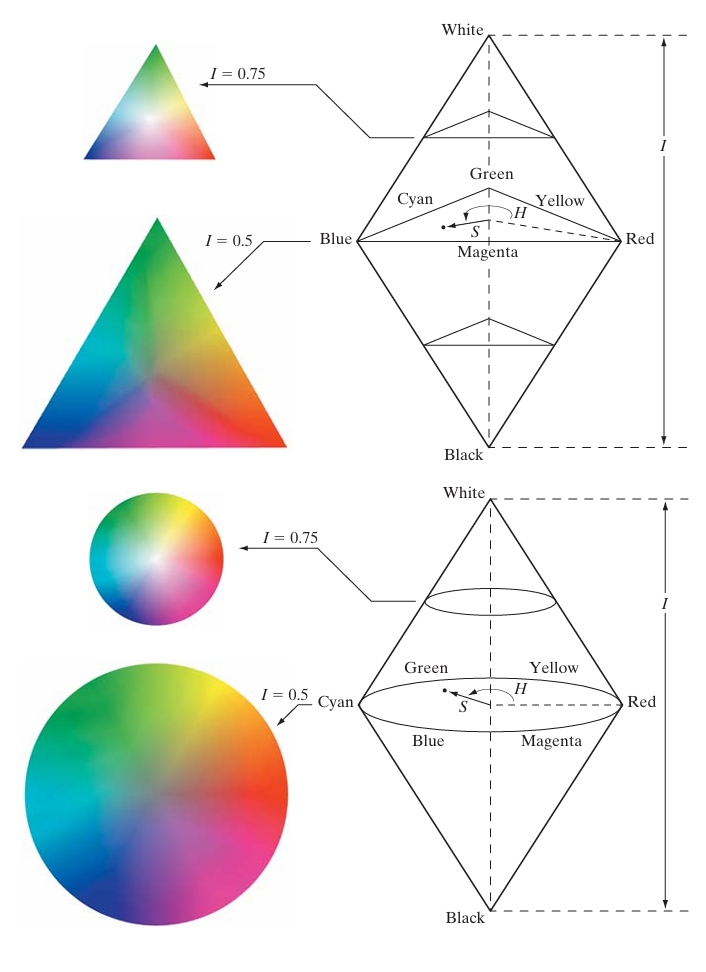
The HSI model is particularly valuable because it mirrors the way people naturally perceive color. By separating intensity (or brightness) from hue and saturation, the model allows for a clearer understanding of how different colors relate to one another. For instance, the model represents the intensity of a color along a vertical axis, with hue and saturation forming a plane that shifts in shape depending on the intensity level. This geometric structure makes it easier to manipulate and describe colors in a way that feels natural for humans.
Furthermore, the HSI model provides a versatile framework for image processing tasks. Since it simplifies the description of colors in terms of how humans perceive them, it is a useful tool for developing algorithms that rely on intuitive color manipulation. Unlike the RGB model, which can be cumbersome for color description, the HSI model enables more effective color interpretation and modification, making it a popular choice for tasks that involve analyzing and processing color images.
Converting colors from RGB to HSI
To obtain the hue (H) component of each pixel in an RGB image, the following equation is used:
where is given by:
The saturation (S) component is calculated as:
Finally, the intensity (I) component is determined by:
It is assumed that the RGB values have been normalized to the range [0, 1], and the hue angle is measured relative to the red axis of the HSI color space. Hue can be further normalized by dividing the resulting value by 360° to map it to the range [0, 1]. The saturation and intensity components are already in this range if the RGB values are within [0, 1].
Converting colors from HSI to RGB
The conversion of colors from HSI (Hue, Saturation, Intensity) to RGB (Red, Green, Blue) is a fundamental process in image processing, where the goal is to translate colors defined by human-perceived characteristics into the RGB model, which is used in digital displays and cameras. The HSI model separates hue (the type of color), saturation (the vividness or purity of the color), and intensity (brightness), which allows for easier manipulation of these aspects, especially for tasks such as color correction or enhancement.
HSI to RGB Conversion Process
To convert HSI values (with H in the range [0°, 360°] and S and I in the range [0, 1]) to RGB, we use a set of equations. The conversion process depends on the value of H, as this determines the color sector in which the hue lies. There are three key sectors, each corresponding to a 120° interval of hue:
- RG sector (0° ≤ H < 120°)
- GB sector (120° ≤ H < 240°)
- BR sector (240° ≤ H ≤ 360°)
RG Sector (0° ≤ H < 120°):
When H lies between 0° and 120°, we calculate the RGB components as follows:
Blue component (B):
This equation indicates that the blue component is determined by the intensity (I) reduced by the saturation (S). A lower saturation means a higher value of blue.
Red component (R):
This formula adjusts the red component based on the hue (H) and saturation (S). The cosine functions help manage the transitions between colors smoothly.
Green component (G):
The green component is computed by subtracting the red and blue components from three times the intensity. This ensures that the total intensity remains consistent.
GB Sector (120° ≤ H < 240°):
When the hue falls between 120° and 240°, the calculation is similar but requires an initial adjustment to H by subtracting 120° to simplify the angle:
- Hue adjustment:
After adjusting H, the RGB components are calculated:
Red component (R):
As in the RG sector, the red component depends on the intensity reduced by the saturation.
Green component (G):
The green component is modified based on the adjusted hue, saturation, and cosine functions, similar to the way red was calculated in the RG sector.
Blue component (B):
The blue component is found by subtracting the sum of the red and green components from three times the intensity.
BR Sector (240° ≤ H ≤ 360°):
For hues between 240° and 360°, another adjustment is made to H, this time subtracting 240°:
- Hue adjustment:
After this adjustment, the RGB components are computed as follows:
Green component (G):
The green component is calculated similarly to the red in the previous sectors.
Blue component (B):
This formula determines the blue component, based on the adjusted hue and saturation.
Red component (R):
The red component is found by subtracting the sum of the green and blue components from three times the intensity.

Example Explanation (Figure 6.15):
Figure 6.15 in the example illustrates how the HSI model represents an image. This figure shows the hue, saturation, and intensity values for each pixel in an image corresponding to the RGB color cube. Each pixel in the HSI representation is related to the corresponding pixel in the RGB color space, but it separates the color information more clearly.
- (a) Hue Image:
This image represents the hue for each pixel. The most noticeable feature is a discontinuity along a 45° line in the red plane of the RGB cube, which reflects a sharp change in color along this line. In HSI terms, this means a sudden transition in hue at this angle. - (b) Saturation Image:
This image shows the saturation values for each pixel. As the values become closer to the white vertex of the RGB cube, they become darker, indicating that the colors are less saturated (closer to white). The level of saturation diminishes toward the white point because colors blend into white as saturation decreases. - (c) Intensity Image:
The intensity image represents the brightness of each pixel. It is essentially the average of the RGB values at each pixel location. Bright pixels in this image correspond to regions where the RGB components have higher combined values, indicating higher brightness.
Manipulating HSI component images


In image processing, manipulating HSI (Hue, Saturation, Intensity) component images is a powerful method that allows us to make targeted adjustments to specific aspects of an image’s color characteristics. By working within the HSI color model, we can modify the hue (the actual color), the saturation (color purity or vividness), and the intensity (brightness) independently, which gives greater flexibility compared to the RGB color model where color and brightness are interdependent.
Overview of the HSI Color Model
The HSI model separates color into three components:
- Hue (H): This defines the actual color, and is measured in degrees (from 0° to 360°) on the color wheel. For example, 0° represents red, 120° represents green, and 240° represents blue.
- Saturation (S): This measures the purity of the color, with 0 representing gray (no color saturation), and 1 representing fully saturated colors.
- Intensity (I): This represents the brightness of the color. It is the average of the RGB values and varies from 0 (black) to 1 (white).
Manipulating HSI Component Images
In this process, we modify the individual H, S, and I components, rather than the RGB values directly. This provides more intuitive control over how colors appear and how bright or dim they are. The manipulation of these components can result in significant changes in the resulting RGB image.
Example of HSI Manipulation
Let’s examine an example based on Figure 6.16, which demonstrates an RGB image and the corresponding HSI components:
Original RGB Image (Figure 6.16(a)):
The image is composed of primary (red, green, blue) and secondary (cyan, magenta, yellow) colors, forming three overlapping circles. This is the original color image that we want to manipulate.Hue Component (H) (Figure 6.16(b)):
The hue image shows the angle corresponding to each color in the original RGB image. In grayscale, black represents areas where hue corresponds to red (0°), while white corresponds to hues closer to yellow, cyan, and green. This image maps the color information but disregards brightness and saturation.Saturation Component (S) (Figure 6.16(c)):
The saturation image shows how vivid the colors are in the original image. Dark regions correspond to areas with low saturation (closer to gray), and brighter regions represent more saturated colors (closer to their pure color). Areas with strong red, green, and blue appear brighter in this image.Intensity Component (I) (Figure 6.16(d)):
The intensity image represents the brightness of each pixel in the original image. White areas indicate high intensity (brightness), while black areas are regions of low intensity.
Mathematical Concepts in HSI Manipulation
To modify any aspect of the image, we adjust one or more of the HSI components and then convert the result back to the RGB color model using the following key equations:
1. Hue Modification:
To change the color in a specific region, we adjust the H value of the pixels corresponding to that region in the hue image.
For example, in Figure 6.17(a), the hue values of the blue and green regions (corresponding to the angles 120° and 240°) have been modified, making them black in the hue image. This change results in a transformation of those regions to a different hue when the image is converted back to RGB.
- Hue adjustment: Where is the new hue angle for the region we want to change. This angle determines the color it will map to in the RGB model.
2. Saturation Modification:
To change the saturation (or purity) of the color in a region, we modify the S value. For example, in Figure 6.17(b), the saturation of the cyan region (which is located between blue and green) has been reduced by half. As a result, that region appears more washed out (closer to gray).
The formula for adjusting saturation is simple:
Where is the new saturation, and the scaling factor determines how much we decrease or increase the saturation. A value of 0 would turn the region gray, while a value of 1 keeps it at full saturation.
3. Intensity Modification:
To modify the brightness of the image, we adjust the I value. In Figure 6.17(c), the intensity in the central white region is reduced by half, making that region darker.
The formula for adjusting intensity is:
Where is the new intensity. If we multiply by a value less than 1, the region becomes dimmer; multiplying by a value greater than 1 would brighten the region.
Reconstructing the RGB Image
After modifying the HSI components, we convert the image back to the RGB color model using the following equations for each color sector:
Conversion from HSI to RGB:
The conversion formulas depend on the hue sector, as described earlier:
RG sector (0° ≤ H < 120°):
GB sector (120° ≤ H < 240°): First, adjust the hue:
Then, compute the RGB components:
BR sector (240° ≤ H ≤ 360°): Adjust the hue:
Then calculate:
Final Example of HSI Manipulation
The result of converting the modified HSI image back to RGB is shown in Figure 6.17(d). In this case, we see the following changes:
- The cyan region’s saturation has been reduced, making it appear more gray.
- The intensity of the central white region has been reduced, dimming that area.
- The outer portions of the circles are now primarily red due to the hue adjustment in those regions.
These changes illustrate the power of the HSI model in allowing independent control over hue, saturation, and intensity—key aspects of image color. By using this method, we can make highly controlled adjustments to images for a variety of applications such as color correction, contrast enhancement, or aesthetic modifications.
References
- Gonzalez, R. C., & Woods, R. E. (2018). Digital Image Processing (4th ed.). Pearson.
- Pratt, W. K. (2007). Digital Image Processing: PIKS Scientific Inside (4th ed.). Wiley.
- Poynton, C. (2012). Digital Video and HDTV: Algorithms and Interfaces. Morgan Kaufmann.
- Foley, J. D., van Dam, A., Feiner, S. K., & Hughes, J. F. (1995). Computer Graphics: Principles and Practice (2nd ed.). Addison-Wesley.
