Color Transformations

by

Color transformations involve processing the components of a color image within a single color model, rather than converting between different models. In these transformations, each pixel of the color image is represented as a triplet (for RGB or HSI) or quartet (for CMYK) of values corresponding to the chosen color space.

Table of Contents

Formulation of Color Transformations

Similar to intensity transformations, a general model for color transformations can be represented by:

g(x,y)=T[f(x,y)]g(x, y) = T[f(x, y)]

Where:

  • f(x,y)f(x, y) is the input color image,
  • g(x,y)g(x, y) is the processed or transformed output image,
  • TT is the transformation operator applied over the image’s spatial neighborhood.

In color images, the pixel values are groups of three (RGB, HSI) or four (CMYK) values. The transformation process often involves applying separate functions for each color component. For instance, in the case of RGB images:

si=Ti(r1,r2,...,rn)s_i = T_i(r_1, r_2, …, r_n)

Here, r1,r2,...,rnr_1, r_2, …, r_n represent the color components of the input image at point (x,y)(x, y), and sis_i are the transformed color components. If the chosen color space is RGB, n=3n = 3 and the three components are red, green, and blue. For CMYK, n=4n = 4 and the components are cyan, magenta, yellow, and black.

Example: Color Transformations in CMYK, RGB, and HSI

Consider a high-resolution color image of strawberries and coffee, digitized from a large-format color negative. The image is first represented in the CMYK color space, where each component (cyan, magenta, yellow, and black) contributes to the overall image. For example, the strawberries in the image show large amounts of magenta and yellow because these components are the brightest. When the image is converted to the RGB space, the strawberries appear predominantly red with minimal green and blue components.

In the HSI (Hue, Saturation, Intensity) space, the intensity component represents a monochrome version of the full-color image, and the strawberries show high saturation due to their pure red color. However, interpreting the hue component can be challenging due to discontinuities where 0° and 360° meet, and the hue is undefined for white, black, and gray colors.

Practical Example: Intensity Modification

Let’s say we want to modify the intensity of the image using the transformation:

g(x,y)=kf(x,y)where0≤k≤1g(x, y) = k f(x, y) \quad \text{where} \quad 0 \leq k \leq 1

This can be done differently depending on the color space. In the HSI color space, only the intensity component is affected:

  • s1=r1s_1 = r_1
  • s2=r2s_2 = r_2
  • s3=kr3s_3 = k r_3

In contrast, the RGB and CMYK spaces require transformations of all components. For RGB:

si=krii=1,2,3s_i = k r_i \quad i = 1, 2, 3

For CMYK:

si=kri+(1−k)i=1,2,3s_i = k r_i + (1 – k) \quad i = 1, 2, 3

Although the HSI transformation involves fewer operations, converting the image to HSI from RGB or CMYK is computationally intense. In this case, it may be more efficient to apply the transformation directly in the RGB or CMYK spaces.

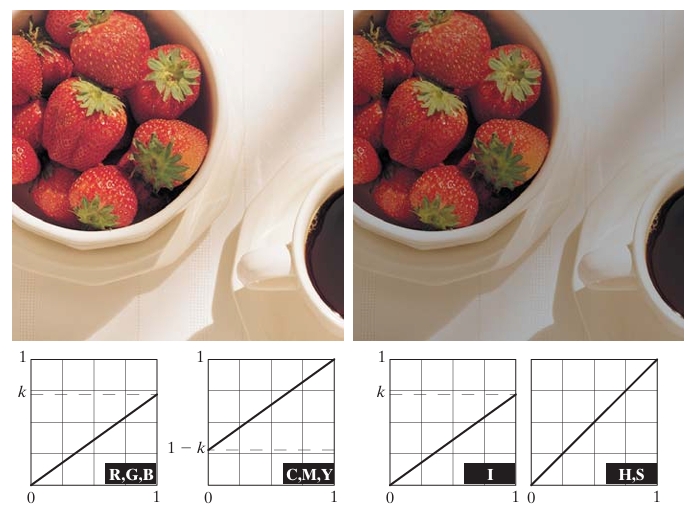
FIGURE 6.31 Adjusting the intensity of an image using color transformations.
(a) Original image.
(b) Result of decreasing its intensity by 30% (i.e., letting k = 0.7).
(c)–(e) The required RGB, CMY, and HSI transformation functions. (Original image courtesy of MedData Interactive.)

Example Output

When we apply an intensity transformation with k=0.7k = 0.7, the result is a darker version of the original image, as shown in Fig. 6.31(b). The transformation functions are depicted graphically in Figs. 6.31(c)-(e), showing how each color component is modified independently.

Color Complements

Color complements refer to hues that are positioned directly opposite each other on a color circle. These complements hold a significant role in image processing, as they are analogous to grayscale negatives, which are helpful for enhancing details in dark areas of a color image. Particularly, color complements are effective when these dark regions dominate the image, allowing important features to be brought out.

Mathematical Concept of Color Complements

In the RGB color model, the complement of a color is determined by subtracting each color component from its maximum value. Since RGB values range from 0 to 255 (for an 8-bit system), the complement of any RGB color C=(R,G,B)\mathbf{C} = (R, G, B) can be computed by:

Ccomplement=(255−R,255−G,255−B)C_{\text{complement}} = (255 – R, 255 – G, 255 – B)

Where:

  • RR, GG, and BB are the red, green, and blue components of the original color,
  • CcomplementC_{\text{complement}} is the complement of the color.

This is essentially the same as the transformation used for grayscale negatives, but applied to each color component independently.

Example:

If you have an RGB color represented by (R,G,B)=(50,100,150)(R, G, B) = (50, 100, 150), the complement would be:

Ccomplement=(255−50,255−100,255−150)=(205,155,105)C_{\text{complement}} = (255 – 50, 255 – 100, 255 – 150) = (205, 155, 105)

In this example, the original color with a slightly bluish tone would become a more reddish tone after applying the complement transformation.

Visualizing Complements on a Color Circle

On a color circle, complementary colors are those positioned directly opposite each other. For instance:

  • Red is opposite Cyan,
  • Green is opposite Magenta,
  • Blue is opposite Yellow.

When a color is complemented, its hue shifts to the opposite side of the circle, which changes its appearance significantly.

Color Complement in Image Processing

Consider the color image shown in Fig. 6.31 (a bowl of strawberries and a cup of coffee). When its complement is computed, the red strawberries turn cyan, and the black coffee becomes white. The result is reminiscent of a photographic film negative. This kind of transformation is particularly useful for enhancing fine details that may otherwise be difficult to discern in dark regions of the image, such as shadows.

Mathematical Example of RGB Transformation for Complements

In this example, let’s take a pixel from the image that has an RGB value of (R,G,B)=(200,50,80)(R, G, B) = (200, 50, 80). To find the complement of this pixel, we apply the complement formula:

Rcomplement=255−200=55R_{\text{complement}} = 255 – 200 = 55 Gcomplement=255−50=205G_{\text{complement}} = 255 – 50 = 205 Bcomplement=255−80=175B_{\text{complement}} = 255 – 80 = 175

Thus, the complement of (200,50,80)(200, 50, 80) is (55,205,175)(55, 205, 175).

Hue-Saturation-Intensity (HSI) and Complements

Unlike the simple RGB complement transformation, computing a complement in the HSI color model is not as straightforward. In RGB, the transformation of each component is independent of the others, but in HSI, components like hue and saturation are interdependent.

For example, the hue complement in HSI is obtained by shifting the hue value by 180° on the color wheel. However, this transformation may not be as simple as in the RGB model because the saturation and intensity of the image play important roles in the final output.

If we take an image with very low saturation (like grayscale or nearly grayscale), its complement may not be perceptible because the hue is poorly defined when the saturation is close to zero. In such cases, a direct HSI transformation for complements can result in unexpected or inaccurate outcomes.

This interdependence in HSI is explored further in the text and left as an exercise to show that the saturation component of the complement cannot be computed solely from the input saturation.

Practical Example: Color Complement Application

Let’s apply the complement transformation to an image. Suppose we have an image where a red object dominates (for instance, strawberries in the earlier example). The RGB value of a red pixel might be something like (R,G,B)=(200,0,0)(R, G, B) = (200, 0, 0).

The complement of this red pixel would be:

Rcomplement=255−200=55R_{\text{complement}} = 255 – 200 = 55 Gcomplement=255−0=255G_{\text{complement}} = 255 – 0 = 255 Bcomplement=255−0=255B_{\text{complement}} = 255 – 0 = 255

So, the complement of a pure red pixel would result in (55,255,255)(55, 255, 255), a cyan color. This transformation is often used to reveal details in the image that are difficult to see in the original due to the dominance of one color.

Color Slicing

Color slicing is a technique used in image processing that isolates and highlights a specific range of colors in an image. This method is particularly useful when the goal is to emphasize a particular object or region in a color image based on its color values. Color slicing can help highlight certain features in an image while reducing or completely suppressing the background or other irrelevant parts.

Mathematical Concept of Color Slicing

In color slicing, the goal is to retain a set of pixels whose colors fall within a specified range (called the “slice”) and suppress (darken or desaturate) all other colors. Mathematically, this is done by selecting a range of colors around a target color CtC_t in a given color space (for instance, the RGB color space), and transforming the pixels that fall within this range.

The color slicing operation is represented as follows:

g(x,y)={f(x,y),if ∥f(x,y)−Ct∥<Δ0,otherwiseg(x, y) = \begin{cases} f(x, y), & \text{if } \| f(x, y) – C_t \| < \Delta \\ 0, & \text{otherwise} \end{cases}

Where:

  • f(x,y)f(x, y) is the color value at pixel (x,y)(x, y) in the input image.
  • g(x,y)g(x, y) is the resulting pixel value at (x,y)(x, y) after color slicing.
  • CtC_t is the target color (the color we want to highlight).
  • Δ\Delta is a threshold that defines the tolerance for the color range around CtC_t.
  • ∥f(x,y)−Ct∥\| f(x, y) – C_t \| is the distance between the pixel’s color and the target color in the chosen color space.

Example: Color Slicing in RGB Space

In the RGB color space, each pixel is represented by a triplet (R,G,B)(R, G, B), where RR, GG, and BB are the red, green, and blue components, respectively. Suppose we want to highlight only red regions in an image. We select a target red color Ct=(Rt,Gt,Bt)=(255,0,0)C_t = (R_t, G_t, B_t) = (255, 0, 0), which represents a pure red color.

We can then define a threshold Δ\Delta to decide how much variation around this red color we will tolerate. For instance, if Δ=50\Delta = 50, any pixel whose RGB values are within a distance of 50 from (255,0,0)(255, 0, 0) will be kept, while others will be darkened or set to zero.

The distance between two colors in RGB space can be calculated using the Euclidean distance:

∥(R,G,B)−(Rt,Gt,Bt)∥=(R−Rt)2+(G−Gt)2+(B−Bt)2\| (R, G, B) – (R_t, G_t, B_t) \| = \sqrt{(R – R_t)^2 + (G – G_t)^2 + (B – B_t)^2}

If this distance is less than Δ\Delta, the pixel’s color is retained; otherwise, it is suppressed.

Example:

Consider an image where a red apple needs to be highlighted, and the background should be suppressed. Let the target red color be Ct=(255,0,0)C_t = (255, 0, 0), and let the threshold Δ=50\Delta = 50.

If a pixel in the image has the color f(x,y)=(250,30,20)f(x, y) = (250, 30, 20), we compute the distance to the target red color as:

∥(250,30,20)−(255,0,0)∥=(250−255)2+(30−0)2+(20−0)2=(−5)2+(30)2+(20)2=25+900+400=1325≈36.4\| (250, 30, 20) – (255, 0, 0) \| = \sqrt{(250 – 255)^2 + (30 – 0)^2 + (20 – 0)^2} = \sqrt{(-5)^2 + (30)^2 + (20)^2} = \sqrt{25 + 900 + 400} = \sqrt{1325} \approx 36.4

Since this distance is less than 50, the pixel is retained.

If a pixel has a color like (100,150,200)(100, 150, 200), the distance calculation would yield:

∥(100,150,200)−(255,0,0)∥=(100−255)2+(150−0)2+(200−0)2=(−155)2+(150)2+(200)2=24025+22500+40000=86525≈294.1\| (100, 150, 200) – (255, 0, 0) \| = \sqrt{(100 – 255)^2 + (150 – 0)^2 + (200 – 0)^2} = \sqrt{(-155)^2 + (150)^2 + (200)^2} = \sqrt{24025 + 22500 + 40000} = \sqrt{86525} \approx 294.1

Since the distance is much larger than 50, this pixel would be suppressed or set to black.

Color Slicing in Different Color Spaces

Color slicing can be performed in different color spaces, including:

  • HSI (Hue, Saturation, Intensity): In the HSI model, the target color is defined by its hue, and color slicing can be done based on hue ranges. This is often more intuitive than RGB for applications where color perception matters (e.g., human visual system).
  • Lab color space: The Lab color space separates the lightness component (L) from the color components (a and b), making it ideal for color slicing based on perceptual color differences.

In the HSI color space, color slicing is typically performed based on the hue value. If you want to highlight a certain hue (e.g., red), you would specify a range of hues around the target hue. The advantage of using HSI is that it allows for easier manipulation of colors while keeping brightness and saturation separate.

Example in HSI Space:

If the target hue for a red object is Ht=0∘H_t = 0^\circ (red), you can define a range of hue values between Ht−ΔHH_t – \Delta H and Ht+ΔHH_t + \Delta H. For example, with ΔH=15∘\Delta H = 15^\circ, any hue between −15∘-15^\circ and +15∘+15^\circ around red would be retained, and other hues would be suppressed.

Applications of Color Slicing

Color slicing has various practical applications:

  1. Medical Imaging: In medical images, certain color ranges (like those associated with tissue types or stains) can be isolated and emphasized to help with diagnosis.
  2. Object Detection: Color slicing can be used to isolate and detect specific objects in an image, such as detecting fruits (e.g., apples) in a scene based on their red color.
  3. Remote Sensing: In satellite imagery, certain natural features (like vegetation) have distinct color signatures, and color slicing can help in isolating these features for analysis.
  4. Digital Art: Artists use color slicing to create visually striking images by highlighting particular colors in a photograph or design while suppressing others.

Tone and Color Corrections

Tone and color corrections are essential processes in modern digital imaging workflows, allowing photographers, graphic designers, and image editors to fine-tune their images for optimal visual appeal and accuracy. These adjustments can be made using standard desktop computers in conjunction with digital cameras, flatbed scanners, and inkjet printers, transforming a personal computer into a digital darkroom. This process eliminates the need for traditional darkroom processing, as tonal adjustments and color corrections can be handled digitally, particularly in photo enhancement and color reproduction.

Importance of Monitors in Color Corrections

To ensure effective tone and color corrections, the transformations must be developed, refined, and evaluated on monitors. It is crucial to maintain a high degree of color consistency between monitors and output devices (such as printers) to ensure that the final output is accurate to the digital representation.

Color Profiles are essential in this process, helping to map each device’s color gamut to a universal color model. For many color management systems (CMS), the model of choice is the CIE Lab model*, also known as CIELAB. This color model relates the colors between devices and represents the entire visible spectrum, ensuring that the colors are perceived consistently across different displays and devices. It is colorimetric, meaning it is designed to ensure perceptual uniformity in color differences.

Mathematical Concepts Behind CIE Lab* Model

The Lab* model represents colors in three dimensions:

  1. L*: Lightness component.
  2. a*: Represents the red-green axis.
  3. b*: Represents the blue-yellow axis.

The components are defined mathematically as:

L∗=116⋅h(YYw)−16(6.5-9)L* = 116 \cdot h\left(\frac{Y}{Y_w}\right) – 16 \tag{6.5-9} a∗=500⋅[h(XXw)−h(YYw)](6.5-10)a* = 500 \cdot \left[ h\left(\frac{X}{X_w}\right) – h\left(\frac{Y}{Y_w}\right) \right] \tag{6.5-10} b∗=200⋅[h(YYw)−h(ZZw)](6.5-11)b* = 200 \cdot \left[ h\left(\frac{Y}{Y_w}\right) – h\left(\frac{Z}{Z_w}\right) \right] \tag{6.5-11}

Where:

  • XX, YY, and ZZ are the tristimulus values of the color in the image.
  • XwX_w, YwY_w, and ZwZ_w are the tristimulus values of a reference white point (typically white from a perfectly diffusing surface under standardized light, like D65 illumination).
  • The function h(q)h(q) is defined as:
h(q)={q1/3if q>0.0088567.787q+16116if q≤0.008856(6.5-12)h(q) = \begin{cases} q^{1/3} & \text{if } q > 0.008856 \\ 7.787q + \frac{16}{116} & \text{if } q \leq 0.008856 \end{cases} \tag{6.5-12}

The transformation is based on the CIE chromaticity diagram, where x=0.3127x = 0.3127 and y=0.3290y = 0.3290, standard values under D65 illumination, representing daylight.

Perceptual Uniformity

One of the main benefits of the Lab* system is perceptual uniformity: differences in color values (between hues) are perceived by the human eye as roughly the same amount of difference. This ensures that color corrections performed using this model will result in consistent visual results across various devices, from monitors to printers. This model is also device-independent, meaning the same values can represent the colors on any display or output device without the need for further transformations.

Example: Color Correction Using Lab*

Consider an image with significant tonal imbalance, where certain parts are overly saturated (too bright) and other areas are undersaturated (too dark). By adjusting the L* component (lightness), you can either brighten or darken specific areas to balance the intensity. Additionally, you can adjust the a* and b* components to correct color shifts (such as from red to green or from blue to yellow).

Suppose a print of an image appears too warm (too red-yellow). By adjusting the a* and b* values towards the negative side (green and blue), the tonal balance can be corrected, making the image appear more neutral.

Tonal Range and Tonal Adjustments

Another crucial aspect of tone correction is adjusting the tonal range of an image. The tonal range refers to the distribution of intensities in an image, from the darkest blacks to the brightest whites. Images with an uneven tonal range (such as high-key images, which have most information concentrated in high intensities, or low-key images, concentrated in low intensities) may require balancing to ensure that details are visible across the entire intensity spectrum.

This process often involves histogram equalization, where the histogram of pixel intensities is adjusted to stretch across the full range of possible values, thereby improving the contrast and revealing details in both the highlights and shadows.

Histogram Processing

Histogram processing is a fundamental technique in image processing, used primarily to enhance the contrast of images. The histogram of an image represents the distribution of pixel intensities, showing how often each intensity value occurs in the image. By analyzing and manipulating this histogram, we can improve the visual quality of an image, making details more visible and improving contrast.

1. What is a Histogram?

For a grayscale image, the histogram is a graph with:

  • The x-axis representing the intensity levels (ranging from 0 to 255 for an 8-bit image).
  • The y-axis representing the frequency of each intensity level (i.e., how many pixels in the image have that intensity value).

The intensity values range from 0 (black) to 255 (white) for an 8-bit grayscale image. The histogram provides a visual representation of how pixel intensities are distributed, which is essential for analyzing an image’s contrast and brightness.

2. Types of Histogram Manipulation

The two most common types of histogram-based processing are Histogram Equalization and Histogram Matching (Specification).

2.1 Histogram Equalization

Histogram equalization is a method to enhance the contrast of an image. It spreads out the most frequent intensity values in an image, making the image appear clearer and more balanced in terms of brightness.

Mathematical Concept

Given an image with LL possible intensity levels, the goal is to map each pixel’s intensity value to a new value based on its cumulative distribution function (CDF) in such a way that the resulting image has a roughly uniform histogram.

Let rkr_k be the kk-th intensity level in the input image, and let p(rk)p(r_k) represent the probability of occurrence of intensity level rkr_k. The histogram equalization transformation function T(r)T(r) is defined as:

T(rk)=(L−1)∑j=0kp(rj)T(r_k) = (L-1) \sum_{j=0}^{k} p(r_j)

Where:

  • LL is the total number of intensity levels (for an 8-bit image, L=256L = 256).
  • p(rj)p(r_j) is the normalized histogram of the image, i.e., the probability of each intensity value occurring in the image.
  • T(rk)T(r_k) is the new intensity value corresponding to rkr_k after equalization.
Steps:
  1. Compute the histogram of the image.
  2. Normalize the histogram to create a probability distribution.
  3. Compute the cumulative distribution function (CDF).
  4. Use the CDF to map each intensity level rkr_k to a new intensity value T(rk)T(r_k).
Example

Suppose we have an image with the following pixel intensities: [52, 55, 61, 59, 79, 61, 64, 64, 73, 85]. The histogram for these pixel values shows that intensities are concentrated in certain areas, so we apply histogram equalization.

  • Step 1: Compute the histogram, showing how often each intensity appears.
  • Step 2: Normalize the histogram by dividing by the total number of pixels.
  • Step 3: Compute the CDF by summing the normalized histogram values.
  • Step 4: Map the pixel values to new values based on the CDF to spread the intensity values evenly.

This process results in a more uniform distribution of intensities and improved contrast in the image.

2.2 Histogram Matching (Specification)

While histogram equalization enhances contrast, it might not always produce the desired effect. Sometimes, we want the output image to have a specific histogram shape (e.g., to match the style of another image). This technique is called histogram matching or specification.

Mathematical Concept

Let rr be the intensity levels in the original image, and zz be the intensity levels in the target image. The goal of histogram matching is to map the intensity values of the original image to the intensity values of the target image so that the histograms of the two images match.

The basic process involves:

  1. Compute the histogram and CDF of the original image.
  2. Compute the histogram and CDF of the target image.
  3. For each intensity level rkr_k in the original image, find the corresponding intensity level zjz_j in the target image using their CDFs.
Steps:
  1. Compute the histograms and CDFs of both the input and target images.
  2. For each intensity value in the input image, find the closest corresponding intensity in the target image using the inverse of the CDF.
  3. Replace each pixel intensity in the input image with the matched intensity from the target image.
Example

Suppose we have two images:

  • The input image has a histogram that is concentrated in the lower intensity range (dark image).
  • The target image has a histogram with a broader distribution of intensities (well-exposed image).

By applying histogram matching, we can adjust the input image’s histogram to match the target image’s histogram. This improves the brightness and contrast of the input image, giving it the appearance of the target image.

3. Applications of Histogram Processing

  • Contrast Enhancement: Histogram equalization is widely used to improve contrast in low-contrast images, making them visually clearer and more detailed.
  • Style Transfer: Histogram matching can be used to give one image the appearance of another, by matching their histograms.
  • Preprocessing for Computer Vision: Many algorithms in computer vision benefit from images with uniform histograms, as it ensures that features in the image are distributed evenly.

4. Example of Histogram Equalization

Let’s take an image that has poor contrast, where most pixel values are clustered around a narrow range of intensity values. The steps for histogram equalization can be applied as follows:

  1. Original Histogram: A typical low-contrast image might have its pixel intensities clustered between 50 and 150 (on a scale of 0-255). The histogram will show this as a spike in the midrange.

  2. Histogram Equalization: By redistributing these pixel intensities using the cumulative distribution function, we spread the pixel values more evenly across the range from 0 to 255. The histogram after equalization will be flatter, and the image will have improved contrast.

5. Limitations of Histogram Processing

  • Over-enhancement: In some cases, histogram equalization can over-enhance the contrast, causing noise or other unwanted artifacts to become more visible.
  • Global Approach: Standard histogram processing techniques are global, meaning they treat all pixels in the image equally. This may not always be desirable, especially if different parts of the image require different adjustments. Local histogram processing techniques can address this limitation.

Additional details about Color Transformations

Color transformations are a critical aspect of digital image processing, enabling manipulation of color characteristics in an image. These transformations involve changing the color values of an image’s pixels in a systematic way to achieve effects like color correction, intensity adjustments, and enhancing specific features. In this article, we will discuss the basic principles, mathematical formulations, and examples of key color transformations, particularly focusing on color spaces such as RGB, HSI, and CIE Lab*.

1. Color Spaces and Representations

Before diving into color transformations, it is important to understand that different color spaces represent color in various ways. A color space defines how color is represented as a set of values or coordinates. The three most commonly used color spaces are:

  • RGB (Red, Green, Blue): A device-dependent color model where each color is represented by combining different intensities of red, green, and blue.
  • HSI (Hue, Saturation, Intensity): A more intuitive color model that separates the chromatic content (hue and saturation) from the luminance (intensity).
  • CIE Lab*: A perceptually uniform color model where L∗L^* represents lightness, a∗a^* represents the red-green axis, and b∗b^* represents the blue-yellow axis.

2. Mathematical Formulation of Color Transformations

2.1 Linear Transformations in the RGB Color Space

In the RGB color space, each pixel in the image has three color components: red (RR), green (GG), and blue (BB). Color transformations can be linear or non-linear. One of the simplest forms of transformation is intensity scaling, where the intensity of each color channel is scaled by a constant factor.

For a linear transformation, the transformed pixel value T(R,G,B)T(R, G, B) can be represented as:

[R′G′B′]=A[RGB]+b\begin{bmatrix} R’ \\ G’ \\ B’ \end{bmatrix} = \mathbf{A} \begin{bmatrix} R \\ G \\ B \end{bmatrix} + \mathbf{b}

Where:

  • A\mathbf{A} is a transformation matrix (e.g., for scaling or rotation).
  • b\mathbf{b} is an optional bias vector (often used for translation or shifting).
  • R′,G′,B′R’, G’, B’ are the transformed color components.
Example: Intensity Adjustment

If we want to reduce the intensity of an image by 30%, we can scale the RGB components using a constant factor k=0.7k = 0.7:

R′=0.7×R,G′=0.7×G,B′=0.7×BR’ = 0.7 \times R, \quad G’ = 0.7 \times G, \quad B’ = 0.7 \times B

This transformation uniformly reduces the intensity of the image, making it darker while preserving the color relationships.

2.2 Color Transformations in the HSI Space

The HSI color model separates chromatic information (hue and saturation) from intensity, which is useful for applications like color-based segmentation, where we want to isolate colors without affecting intensity.

The conversion between RGB and HSI is given by the following transformations:

  • Hue (H): Represents the type of color, and is calculated as:
H=cos⁡−1(0.5[(R−G)+(R−B)](R−G)2+(R−B)(G−B))H = \cos^{-1} \left( \frac{0.5 \left[ (R – G) + (R – B) \right]}{\sqrt{(R – G)^2 + (R – B)(G – B)}} \right)
  • Saturation (S): Indicates the purity of the color, and is given by:
S=1−3(R+G+B)min⁡(R,G,B)S = 1 – \frac{3}{(R + G + B)} \min(R, G, B)
  • Intensity (I): Represents the brightness, calculated as:
I=13(R+G+B)I = \frac{1}{3}(R + G + B)
Example: Changing Intensity in HSI

To reduce the brightness of an image, we can modify the intensity component while leaving the hue and saturation unchanged:

I′=k×I,k<1I’ = k \times I, \quad k < 1

This would darken the image while maintaining the color tone and saturation. For instance, setting k=0.8k = 0.8 reduces the intensity by 20%.

2.3 Color Transformations in the CIE Lab Space*

The CIE Lab* (or Lab) color space is perceptually uniform, meaning that changes in color are perceived uniformly by the human eye. This is ideal for tasks like color balancing and color correction.

  • Lightness (L*): Represents the luminance or brightness of the color.
  • a*: Represents the position between green and red.
  • b*: Represents the position between blue and yellow.

The conversion between RGB and CIE Lab* involves an intermediate conversion to XYZ color space, which models human color perception. The formula for converting from XYZ to Lab* is as follows:

L∗=116⋅f(YYw)−16L^* = 116 \cdot f\left( \frac{Y}{Y_w} \right) – 16 a∗=500⋅[f(XXw)−f(YYw)]a^* = 500 \cdot \left[ f\left( \frac{X}{X_w} \right) – f\left( \frac{Y}{Y_w} \right) \right] b∗=200⋅[f(YYw)−f(ZZw)]b^* = 200 \cdot \left[ f\left( \frac{Y}{Y_w} \right) – f\left( \frac{Z}{Z_w} \right) \right]

Where Xw,Yw,ZwX_w, Y_w, Z_w are the reference white tristimulus values, and the function f(q)f(q) is defined as:

f(q)={q1/3,if q>0.0088567.787q+16116,if q≤0.008856f(q) = \begin{cases} q^{1/3}, & \text{if } q > 0.008856 \\ 7.787q + \frac{16}{116}, & \text{if } q \leq 0.008856 \end{cases}
Example: Color Balancing Using Lab*

To balance the color of an image, we can modify the a* and b* components without altering the lightness. For instance, increasing a∗a^* shifts the color towards red, while decreasing it shifts it towards green. Similarly, adjusting b∗b^* shifts the color along the blue-yellow axis.

By tuning these values, we can correct color imbalances, such as removing a yellowish tint from an image by decreasing b∗b^*.

3. Applications of Color Transformations

  • Image Enhancement: Adjusting color intensity and saturation to improve visual appeal, making an image more vibrant.
  • Color Correction: Used in photography and video post-processing to correct color casts, such as white balancing or fixing underexposed regions.
  • Medical Imaging: Color transformations are used to highlight certain features in medical images, such as tumors or abnormalities.
  • Remote Sensing: Used to enhance satellite images by applying color transforms to distinguish land from water, or vegetation from urban areas.

4. Practical Example: Adjusting Intensity in the RGB and HSI Spaces

Consider an image where the overall brightness needs adjustment, but we want to preserve color details. We can:

  1. Convert the image from RGB to HSI.
  2. Adjust only the intensity component.
  3. Convert the image back from HSI to RGB.

The advantage of this method is that the intensity is changed without affecting the hue and saturation, thus preserving the color integrity of the image while adjusting brightness.

References:

  1. Gonzalez, R. C., & Woods, R. E. (2008). Digital Image Processing (3rd ed.). Prentice Hall.
  2. Sharma, G. (Ed.). (2002). Digital Color Imaging Handbook. CRC Press.
  3. Poynton, C. A. (2012). Digital Video and HD: Algorithms and Interfaces. Elsevier.
  4. Robertson, A. R. (1977). The CIE 1976 Color-Difference Formulae. Color Research & Application, 2(1), 7-11.

Leave a Comment