In mathematics, functions of one variable often serve as a foundation for understanding more complex phenomena. However, many real-world problems, particularly in physics, engineering, and computer science, require us to work with functions of two or more variables. A function of two variables, typically written as , takes two independent inputs and produces a single output. This extension to functions of two variables allows us to model surfaces, images, fluid flow, temperature distributions, and much more.
The study of functions of two variables introduces several new concepts compared to single-variable functions, such as partial derivatives, double integrals, and vector fields. These concepts help us analyze the rate of change and accumulation in multiple directions, providing deeper insights into multidimensional systems.
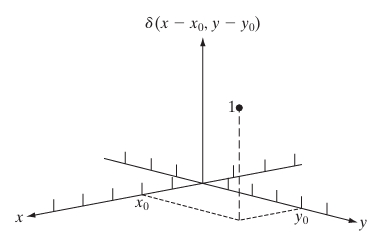
The 2-D Impulse and Its Sifting Property
The 2-D impulse function is denoted as and can be thought of as an extension of the 1-D Dirac delta function . It is a function of two variables, and , which satisfies the following conditions:
- The 2-D impulse function is zero everywhere except at the origin, i.e., :
- The integral of over the entire 2-D space is one:
Thus, the 2-D impulse function is a mathematical model of an idealized point in the 2-D plane, concentrated entirely at the origin, with zero width and infinite height in such a way that its total integral remains 1.
2. Properties of the 2-D Impulse Function
The 2-D impulse has several important properties that are direct extensions of the 1-D Dirac delta function:
a) Shifting Property:
The 2-D impulse function can be shifted from the origin to any point . This shifted impulse is denoted as , and it “spikes” at the location in the 2-D plane:
b) Sifting Property:
The sifting property is one of the most important features of the impulse function. It allows the impulse to “pick out” the value of a function at a specific point. If is a continuous function of two variables, the 2-D impulse function has the following property:
This property tells us that multiplying a function by a shifted 2-D impulse function and integrating over all space results in the value of the function at the location .
3. The Sifting Property of the 2-D Impulse
The sifting property allows us to extract the value of a function at a specific location. This is extremely useful in signal processing and image processing, where functions represent 2-D signals (such as images), and the impulse function acts as a point operator.
Let’s consider a function , which could represent the brightness values of an image at coordinates . The sifting property of the 2-D impulse function allows us to select the value of the image at a specific pixel location, say .
Sifting Property in Detail:
Given a function and a 2-D impulse function centered at , the sifting property is expressed as:
This works because the impulse function is zero everywhere except at , where it is infinite in such a way that the integral picks out the value .
4. Example: Applying the 2-D Impulse and Sifting Property
Example 1: Point Extraction in an Image
Let represent a grayscale image, where gives the brightness at each point . The value of the image at a specific pixel location can be extracted using the 2-D impulse:
This operation is like zooming in on a single pixel and reading its value directly. The impulse function allows us to isolate and focus on specific points in a 2-D domain.
Example 2: Sampling in 2-D
In image processing, sampling refers to capturing the value of a function at discrete points. Using a 2-D array of impulses, we can sample a continuous image . Let’s say we want to sample the function at points , using the following set of impulses:
Multiplying the function by this sum and integrating yields the values of the function at the sample points:
This equation shows how impulses can be used to sample a continuous function at specific locations in 2-D space.
5. Practical Applications
a) Image Processing
In image processing, the 2-D impulse function is used to model operations like sampling, convolution, and filtering. When dealing with image kernels (such as edge detectors), the impulse response of a system is often studied to understand how the system behaves with signals. The sifting property is fundamental in extracting pixel values and performing mathematical operations on images.
b) Signal Processing
The 2-D impulse function is critical in signal processing for systems that handle 2-D signals, such as radar and sonar systems. These systems often model point sources and use impulses to describe the response of the system to specific inputs.
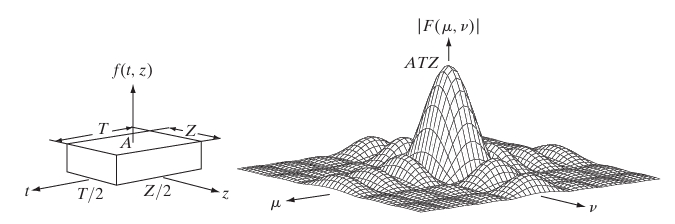
The 2-D Continuous Fourier Transform Pair
The 2-D Continuous Fourier Transform (2D-FT) is an extension of the 1D Fourier transform into two dimensions, allowing us to analyze signals or functions that vary in both the horizontal and vertical directions. This is particularly useful for processing images, where each pixel value represents a function in a 2D plane.
The Fourier transform converts a spatial domain signal (like an image) into its frequency domain representation. This is critical in image analysis, filtering, and signal processing.
Mathematical Concepts
1. 2D Fourier Transform (Forward Transform)
The 2D continuous Fourier transform of a function in the spatial domain is given by:
Where:
- is the function in the spatial domain (typically representing an image or signal).
- is the function in the frequency domain.
- and are the frequency variables corresponding to the horizontal and vertical spatial frequencies.
- is the imaginary unit ().
- is the complex exponential, which encodes both amplitude and phase information in the frequency domain.
2. Inverse 2D Fourier Transform
The inverse transform is used to recover the original spatial domain function from its frequency domain representation:
This equation reconstructs the original spatial domain function from its frequency domain version .
3. Key Properties of the 2D Fourier Transform
- Linearity: The transform of a sum of functions is the sum of their transforms.
- Shift Property: A shift in the spatial domain results in a phase shift in the frequency domain.
- Scaling: A scale in the spatial domain results in an inverse scaling in the frequency domain.
- Convolution: The Fourier transform of a convolution in the spatial domain is the product of their transforms in the frequency domain.
These properties make the 2D Fourier transform very useful in practical applications like image filtering and pattern recognition.
Example: Fourier Transform of a 2D Gaussian Function
Consider a 2D Gaussian function:
This is a symmetric, bell-shaped function in the spatial domain. We will calculate its Fourier transform.
The 2D Fourier transform of the Gaussian function is:
To simplify this, we can take advantage of the fact that the Gaussian function is separable, meaning it can be factored into independent functions of and :
Each of these integrals is a known result from Fourier theory for a Gaussian function. The Fourier transform of a 1D Gaussian is another Gaussian, specifically:
Thus, the 2D Fourier transform of is:
Interpretation
- The 2D Gaussian in the spatial domain transforms into another Gaussian in the frequency domain.
- The width of the Gaussian in the spatial domain is inversely proportional to the width of the Gaussian in the frequency domain. This illustrates the uncertainty principle, which states that a function cannot be both sharply localized in space and sharply localized in frequency.
Applications of 2D Fourier Transform
- Image Processing: The 2D Fourier transform is widely used to analyze the frequency components of images for filtering, compression, and edge detection.
- Optics: In optical systems, the Fourier transform describes how lenses and mirrors affect light waves.
- Pattern Recognition: By examining the frequency content of images, patterns can be detected and classified.
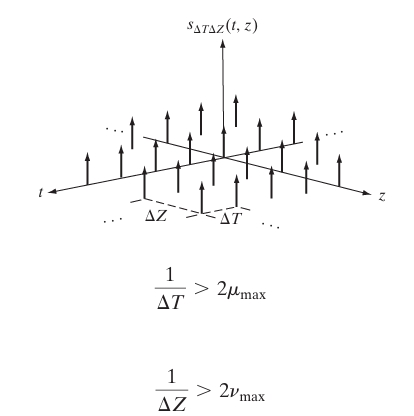
Two-Dimensional Sampling and the 2-D Sampling Theorem
Sampling is the process of converting a continuous signal into a discrete one by measuring its values at regular intervals. In two dimensions (such as in images), sampling means taking measurements at regular points on a 2D grid, converting a continuous 2D function (like an image or a surface) into a discrete set of data points.
In the context of digital image processing, two-dimensional sampling involves recording pixel values at regular intervals in the spatial domain. However, there are some mathematical principles to follow to ensure that the continuous signal can be accurately reconstructed from its sampled version. This is where the 2D Sampling Theorem comes in.
1. Two-Dimensional Sampling Process
In 2D, a continuous signal is sampled at discrete intervals, both in the -direction and -direction. The sampled signal is given by:
Where:
- and are the sampling intervals in the – and -directions.
- and are integers representing the discrete sampling indices.
- is the 2D Dirac delta function, representing the location of the samples in the continuous plane.
The goal of sampling is to ensure that this sampled signal contains all the information needed to reconstruct the original continuous signal without any loss.
2. 2D Sampling Theorem
The 2D Sampling Theorem extends the principles of the 1D Sampling Theorem (also known as the Nyquist-Shannon Sampling Theorem) to two dimensions. It provides conditions under which a continuous 2D signal can be perfectly reconstructed from its samples.
Theorem Statement:
If a 2D continuous signal is band-limited, meaning its Fourier transform has finite support and is zero outside a certain frequency range, then the signal can be perfectly reconstructed from its samples, provided the sampling rate meets or exceeds the Nyquist rate.
Nyquist Rate in 2D:
The Nyquist rate in two dimensions depends on the highest frequency components in both the – and -directions. Let:
- be the highest frequency in the horizontal direction.
- be the highest frequency in the vertical direction.
The Nyquist sampling intervals in the – and -directions are:
This means that the signal must be sampled at least twice the maximum frequency in each direction to avoid aliasing, a phenomenon where high-frequency components are misrepresented as lower frequencies in the sampled signal.
3. Aliasing in 2D
If the sampling rate is too low (i.e., below the Nyquist rate), aliasing occurs. In 2D, aliasing manifests as unwanted patterns or distortions in an image, where higher-frequency components “fold” back into the frequency range that can be represented by the sampled data.
Mathematically, aliasing happens when the Fourier transform of the sampled signal contains overlaps between different copies of the original spectrum, which arise from the periodic nature of sampling.
4. 2D Fourier Domain Representation of Sampling
In the frequency domain, the 2D Fourier transform of a sampled signal is given by:
Where is the Fourier transform of the original continuous signal . The sampling process results in a replication of the original spectrum at intervals of and in the frequency domain.
If the sampling intervals and are too large (i.e., if the sampling rate is too low), the replicated spectra overlap, causing aliasing. If and meet the Nyquist criteria, the replicas do not overlap, and the original signal can be perfectly reconstructed.
5. Reconstruction of the Original Signal
To reconstruct the original continuous signal from the sampled signal, we apply a low-pass filter in the frequency domain that isolates the original spectrum and removes the replicated (aliased) spectra.
In the spatial domain, this reconstruction can be expressed as an interpolation process, where the continuous signal is estimated from the discrete samples using an interpolation function, such as the sinc function, which corresponds to ideal low-pass filtering in the frequency domain.
The reconstructed signal is given by:
6. Example
Consider a 2D sinusoidal signal:
This signal has frequency components at and . To sample this signal without aliasing, we must use sampling intervals that satisfy the Nyquist criterion:
If we sample at these intervals, we can perfectly reconstruct the original sinusoidal signal. However, if we use larger intervals (lower sampling rates), aliasing will occur, and the reconstructed signal will be distorted, with lower-frequency components appearing in the signal.
7. Applications of 2D Sampling
- Image Processing: Digital cameras and scanners use 2D sampling to convert continuous images into pixel data. The 2D Sampling Theorem ensures that images are sampled at a high enough resolution to prevent aliasing.
- Medical Imaging: Techniques like MRI and CT scans rely on 2D sampling to reconstruct continuous images of the human body from discrete measurements.
- Computer Graphics: Texture sampling in 3D rendering uses 2D sampling techniques to apply textures to surfaces without aliasing artifacts.
Aliasing in Images
Aliasing in images is a phenomenon that occurs when a continuous image is sampled at a rate insufficient to capture the detail present in the image, leading to visual artifacts such as jagged edges, moiré patterns, or other distortions. This effect arises due to the inherent limitations of converting a continuous signal (the real-world image) into a discrete one (the digital image).
To fully grasp aliasing, we must delve into the mathematical concepts of signal processing, particularly the Nyquist-Shannon sampling theorem, and understand how sampling and reconstruction affect image quality.
Nyquist-Shannon Sampling Theorem
The Nyquist-Shannon sampling theorem is a fundamental principle that dictates the conditions under which a continuous signal can be perfectly reconstructed from its samples. It states that:
An analog signal that has been sampled can be perfectly reconstructed from its samples if the sampling frequency is greater than twice the highest frequency of the signal.
Mathematically, if the highest frequency component of a signal is , then the sampling frequency must satisfy:
The minimum required sampling frequency is known as the Nyquist rate.
Sampling in One Dimension
Before extending to images, let’s consider a one-dimensional continuous-time signal . When sampled at intervals , we obtain a discrete-time signal:
The sampling frequency is .
Frequency Domain Representation
The Fourier transform of the continuous signal is , representing its frequency content.
Sampling in the time domain corresponds to convolution in the frequency domain. The sampled signal’s Fourier transform is:
This equation shows that the original spectrum is replicated at intervals of along the frequency axis.
Aliasing Occurs When
If , the replicated spectra overlap, causing high-frequency components to masquerade as lower frequencies in the sampled signal. This overlap is the essence of aliasing.
Extension to Two Dimensions (Images)
An image can be represented as a two-dimensional continuous function , where and are spatial coordinates.
Sampling in Spatial Domain
Sampling the image at intervals and along the and axes, respectively, we obtain:
Where represents the Dirac delta function.
Frequency Domain Representation
Applying the two-dimensional Fourier transform, the frequency representation of the sampled image is:
Here, is the Fourier transform of , and are spatial frequency variables.
Aliasing in Images
Aliasing occurs when the replicated spectra overlap due to insufficient sampling rates and . High-frequency details in the image exceed the Nyquist frequency and fold back into lower frequencies, creating distortions.
Visual Manifestations of Aliasing
Moiré Patterns
- Description: When fine patterns in the image interfere with the pixel grid, creating new patterns not present in the original scene.
- Mathematical Cause: Superposition of high-frequency components exceeding Nyquist frequency, leading to beat frequencies.
Jagged Edges (Staircase Effect)
- Description: Diagonal or curved lines appear as a series of steps rather than smooth transitions.
- Mathematical Cause: Insufficient resolution to represent the high spatial frequencies of edges accurately.
Texture Loss
- Description: Fine textures become distorted or disappear entirely.
- Mathematical Cause: High-frequency components are misrepresented due to undersampling.
Anti-Aliasing Techniques
To mitigate aliasing, we can employ strategies in both the sampling and pre-processing stages.
Pre-Filtering (Low-Pass Filtering)
Purpose: Remove high-frequency components that cannot be properly sampled.
Mathematical Operation:
Where is a low-pass filter kernel, and denotes convolution.
Effect in Frequency Domain: Attenuates frequencies above the Nyquist limit, reducing spectral overlap.
Increasing Sampling Rate
- Purpose: Capture more detail by sampling at a higher resolution.
- Mathematical Implication: Increases and , thus expanding the range of frequencies that can be accurately represented.
Post-Filtering (Reconstruction Filtering)
- Purpose: Smooth out artifacts after sampling.
- Methods: Employ interpolation techniques like bilinear or bicubic interpolation.
Mathematical Example
Consider a Continuous Image with a Sinusoidal Pattern
Let the image contain a sinusoidal grating:
Where and are the spatial frequencies along the and axes.
Sampling the Image
Sampling intervals are and , leading to sampling frequencies and .
Aliasing Condition
Aliasing occurs if:
Aliased Frequency Calculation
The aliased frequencies and can be calculated using:
Similarly for .
Example with Numerical Values
Suppose:
- cycles/mm
- samples/mm
Since cycles/mm and cycles/mm, aliasing occurs.
Calculating :
Aliased frequency:
The sampled image will incorrectly represent the frequency as 2 cycles/mm instead of 3 cycles/mm.
Practical Implications
- Image Sensors: Camera sensors have a fixed number of pixels; capturing high-frequency details beyond their capacity leads to aliasing.
- Display Devices: Monitors with limited resolution can introduce aliasing when displaying high-resolution images.
Anti-Aliasing Filters in Cameras
Many cameras incorporate an optical low-pass filter (OLPF) in front of the sensor.
- Function: Blurs the image slightly to remove high-frequency details that cannot be accurately sampled.
- Trade-Off: While it reduces aliasing, it can also soften the image.
Reconstruction of the Image
When displaying or processing the sampled image, reconstruction filters help to mitigate aliasing artifacts.
- Ideal Reconstruction: Sinc function interpolation, which is impractical due to infinite support.
- Practical Reconstruction: Use filters with finite support like Lanczos or Gaussian filters.
Extension from 1-D aliasing
Aliasing, as discussed in one dimension (1-D), occurs when a continuous signal is sampled at a rate lower than the Nyquist rate, resulting in high-frequency components being misrepresented as lower frequencies. This concept extends naturally to two dimensions (2-D), which is crucial for understanding how aliasing manifests in images and other 2-D signals, such as textures or surfaces.
In this extended discussion, we’ll explore how 1-D aliasing principles translate to 2-D, focusing on image sampling, frequency domain analysis, and how aliasing impacts digital images.
1. From 1-D to 2-D Signals
1-D Signal
In 1-D, a continuous-time signal is sampled at intervals to produce a discrete-time signal:
If the sampling frequency is less than twice the highest frequency present in , aliasing occurs.
2-D Signal (Images)
In 2-D, a continuous image is sampled at discrete points , where and , with and being the sampling intervals in the and directions, respectively.
The sampled image is then:
Key Difference: In 2-D, we deal with two sampling frequencies, one along each axis:
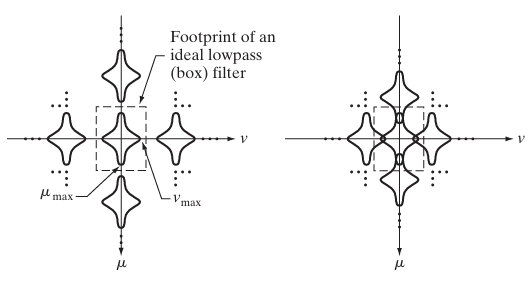
For proper sampling and to avoid aliasing, the sampling frequencies must satisfy the Nyquist criterion in both directions:
Where and are the highest spatial frequencies in the – and -directions, respectively.
2. Frequency Domain Representation in 2-D
Fourier Transform in 1-D
In the 1-D case, a signal’s frequency content is analyzed using the Fourier transform. The Fourier transform of the continuous signal gives its frequency representation . Sampling causes periodic replication of the frequency spectrum at intervals of the sampling frequency .
Fourier Transform in 2-D
In 2-D, the Fourier transform of a continuous image gives its frequency representation , where and are the spatial frequency variables corresponding to the – and -directions.
Sampling in 2-D causes the image’s spectrum to replicate periodically in both frequency directions. The Fourier transform of the sampled image is given by:
This equation shows that the continuous spectrum is replicated at intervals and in the frequency domain. If the sampling frequencies and are too low, these replicas will overlap, leading to aliasing.
3. Aliasing in 2-D Images
Visual Manifestation of Aliasing in 2-D
- Jagged Edges (Staircase Effect): Diagonal lines and curves appear as jagged steps rather than smooth transitions. This occurs when the image contains high-frequency components that the sampling grid cannot accurately capture.
- Moiré Patterns: Interference patterns appear when fine textures interact with the pixel grid. Moiré patterns arise due to overlapping frequency components caused by undersampling.
- Loss of Detail: Fine details, especially in textures and small patterns, may disappear or become misrepresented when sampled at too low a frequency.
Aliasing in the Frequency Domain
In the frequency domain, aliasing results from spectral overlap caused by undersampling. The continuous spectrum is periodically replicated due to sampling, and if the sampling frequencies are insufficient, these replicas overlap with the original spectrum. This overlap causes high-frequency components to be misrepresented as lower frequencies, creating visual distortions.
4. Mathematical Explanation of 2-D Aliasing
To further explain 2-D aliasing mathematically, let’s consider a 2-D sinusoidal pattern in an image:
Where and are the spatial frequencies in the – and -directions, respectively.
Sampling the Image
The image is sampled at intervals and , with sampling frequencies and .
Aliasing occurs when:
That is, if the image contains frequency components higher than half the sampling frequency in either direction, those components will be misrepresented due to aliasing.
Aliased Frequency Calculation
The apparent (or aliased) frequency in the -direction can be computed as:
Where is an integer that minimizes . Similarly, in the -direction, the aliased frequency is:
Where is an integer.
5. Practical Example: Aliasing in Digital Images
Example: Consider an image of a checkered pattern with alternating black and white squares. The spatial frequency of this pattern is determined by how close the squares are together. If this image is sampled with too few pixels per square, aliasing will occur.
- Before Sampling: The original image has high-frequency components corresponding to the sharp transitions between the black and white squares.
- After Sampling (Aliasing): If the sampling rate is too low, these high-frequency components will fold back into the lower frequencies, resulting in a distorted checkered pattern. You might see patterns that do not exist in the original image, such as unwanted stripes or grids.
6. Avoiding Aliasing in 2-D
To prevent aliasing, two primary techniques can be employed:
Increase Sampling Rate
- The simplest method is to increase the sampling frequency along both axes, ensuring that the Nyquist criterion is met in both directions:
Pre-Filtering (Low-Pass Filtering)
- Before sampling, apply a low-pass filter to the image to remove high-frequency components that exceed the Nyquist limit. This ensures that the image’s frequency content is limited to what can be properly represented by the sampling grid.
Image interpolation and resampling
Image interpolation and resampling are key concepts in digital image processing, particularly when you want to change the size of an image, rotate it, or perform other geometric transformations. These processes involve estimating new pixel values when modifying the image’s spatial resolution or dimensions.
Let’s break down each concept:
1. Resampling
Resampling refers to the process of changing the number of pixels in an image. This can either involve:
- Upsampling (increasing the number of pixels), where new pixel values must be estimated (interpolated).
- Downsampling (decreasing the number of pixels), where some pixels are discarded, and the remaining ones are used to approximate the original image.
Example of Resampling: Suppose you have an image that is 4×4 pixels, and you want to increase its size to 8×8 pixels. This process requires estimating new pixel values for the additional pixels, which leads to interpolation.
2. Image Interpolation
Interpolation is the mathematical process used during resampling to estimate the values of new pixels. There are several common methods used in image interpolation:
2.1 Nearest-Neighbor Interpolation
This is the simplest form of interpolation, where the value of a new pixel is assigned based on the value of the closest pixel in the original image. No complex calculations are needed, but this can lead to blocky or pixelated results, especially when upsampling.
Mathematical Concept:
For a pixel at position in the new image, the value is simply taken from the closest pixel in the original image. Let’s say the original image has pixel values , then:
Where and are the nearest integer pixel positions in the original image.
Example:
If you upsample an image from 4×4 to 8×8, for each new pixel, you find the nearest pixel in the original 4×4 image and assign that value directly.
2.2 Bilinear Interpolation
Bilinear interpolation considers the closest 2×2 neighborhood of known pixel values around the new pixel and computes a weighted average. This results in smoother images than nearest-neighbor interpolation.
Mathematical Concept:
For a pixel at position , the value is determined by a weighted average of the four surrounding pixels. If are the coordinates of the four neighboring pixels, the new pixel value is calculated as:
Where are the interpolation weights based on the distance of from each of the four original pixels.
Example:
If you’re upsampling from 4×4 to 8×8, for each new pixel, you take a weighted average of the four closest pixels in the 4×4 image, resulting in a smoother image.
2.3 Bicubic Interpolation
Bicubic interpolation takes into account the 4×4 neighborhood of pixels surrounding the new pixel. It fits a smooth curve based on the 16 surrounding pixels, producing even smoother results than bilinear interpolation, especially for high-quality enlargements.
Mathematical Concept:
Bicubic interpolation is more complex and involves third-degree polynomials to fit curves to the pixel values. The pixel value is computed as a weighted sum of the 16 neighboring pixels, using cubic convolution.
Where the weights are calculated based on cubic interpolation functions, such as a cubic Hermite spline.
Example:
If you increase a 4×4 image to 8×8, for each new pixel, bicubic interpolation would use 16 surrounding pixels from the original image to compute a smoother pixel value than bilinear interpolation.
3. Applications of Interpolation and Resampling
- Zooming: Enlarging an image (upsampling) involves interpolation to estimate pixel values for the new, larger image.
- Rotation and Skewing: These operations often require resampling and interpolation since the original pixel grid is modified.
- Image Compression: Reducing the size of an image (downsampling) involves discarding pixel information and can use interpolation techniques to improve the quality of the compressed image.
4. Example: Upsampling an Image Using Bilinear Interpolation
Let’s take an example where we upsample a 2×2 pixel image to a 4×4 image using bilinear interpolation:
Original 2×2 Image:
Step 1: Find the New Pixel Positions
The new 4×4 image will have more pixel positions. Bilinear interpolation will calculate pixel values for the new positions based on the surrounding 2×2 pixels.
Step 2: Interpolate for New Pixels
The value of a pixel in the new 4×4 image (e.g., pixel at ) will be calculated as the weighted average of the surrounding four pixels from the original 2×2 image.
- New pixel at would take values from the original pixels (10, 20, 30, 40) and compute a weighted average.
Moiré patterns
Moiré patterns are complex interference patterns that arise when two grids or repetitive structures overlap with each other at certain angles or distances. These patterns can appear in various fields, such as in digital imaging, physics, textiles, and even in art. The patterns typically look like ripples, waves, or concentric circles and can be visually striking.
1. What Are Moiré Patterns?
Moiré patterns are essentially optical artifacts created when two sets of similar repetitive structures (like lines, dots, or grids) overlap, and slight differences in angle, spacing, or size cause interference effects.
- If you’ve ever looked at a computer screen through a mesh, or seen strange wave-like patterns when scanning or photographing printed materials (like halftone images), you’ve observed Moiré patterns.
- These patterns are not part of the original image or structure but are generated through the interaction of overlapping elements.
2. Mathematical Concept Behind Moiré Patterns
The creation of Moiré patterns can be explained using interference principles and mathematical concepts of periodicity and superposition.
2.1 Superposition of Two Periodic Patterns
Let’s consider two sets of periodic lines or grids with slightly different spacing or orientation:
- Pattern A: A set of parallel lines with spacing .
- Pattern B: Another set of parallel lines with spacing , either slightly different in spacing or tilted at an angle.
When these two sets are overlaid, the lines will either align or partially align in some regions, but in other regions, they will interfere with each other. The result is a new pattern that appears as if there are large-scale oscillations, even though both original patterns are on a finer scale.
Mathematical Representation:
For simplicity, imagine the lines are one-dimensional and described by sinusoidal functions (which can model repetitive patterns like stripes):
- Pattern A:
- Pattern B:
The combined intensity (or interference pattern) will be represented by the sum of the two functions:
Using trigonometric identities, we can express this as:
This equation shows two components:
- The fast oscillation component (related to the fine periodic structures),
- The slow oscillation component (related to the interference pattern), which gives rise to the Moiré pattern.
2.2 Moiré Frequency
The frequency of the resulting Moiré pattern is given by the difference between the frequencies of the two original patterns. If the spatial frequency of pattern A is and the frequency of pattern B is , the resulting Moiré frequency is:
This equation shows that even a small difference in spacing between the two patterns can produce large-scale Moiré patterns with a lower frequency.
3. Moiré Patterns in Digital Imaging
In digital imaging, Moiré patterns often arise due to the interaction between the sampling grid of a camera sensor and the fine details of a scene (like striped fabrics or printed patterns). This can happen when the resolution of the sensor does not adequately capture the fine details of the subject, leading to interference.
Example: Scanning a Printed Image
- Printed images, such as in magazines or newspapers, often use halftone patterns. This means the image is composed of tiny dots.
- When you scan such an image, the scanning grid may interfere with the halftone dots, leading to a Moiré pattern.
The scanner’s sampling rate can produce periodic structures that interfere with the halftone pattern, creating Moiré effects. The Moiré frequency depends on the relationship between the scanner’s resolution and the spacing of the halftone dots.
Anti-aliasing Filters:
In digital cameras, anti-aliasing filters (or low-pass filters) are often used to reduce Moiré patterns. These filters blur the image slightly to prevent high-frequency details from interacting with the sensor’s pixel grid.
4. Moiré Patterns in Physical Structures
Moiré patterns also appear in physical systems, such as in textiles, optics, and even in materials science.
Example: Overlapping Meshes
Suppose you have two fine mesh grids, one overlaid on top of the other. If the grids are slightly misaligned or rotated relative to each other, Moiré patterns will appear as large-scale waves or ripples.
- If the meshes have similar spacing between the wires, the Moiré pattern will have a low frequency.
- If the spacing is more different, the Moiré pattern will be denser.
Rotation and Moiré Patterns:
When two identical grids are overlaid but rotated by an angle , the Moiré pattern changes based on the angle. As increases, the frequency of the Moiré pattern increases.
5. Example: Moiré Patterns in Textiles
In textiles, Moiré patterns can appear when two layers of fabric with regular patterns, such as stripes or grids, overlap.
Example: Overlapping Striped Fabrics
Imagine you have two pieces of striped fabric, each with stripes at regular intervals and . When you layer the fabrics and slightly rotate one piece, Moiré patterns will appear as new, larger wave-like structures.
The visual pattern can be explained by the same interference formula:
Where and are the stripe frequencies of the two fabrics.
6. Applications of Moiré Patterns
Moiré patterns have practical applications in various fields, including:
- Metrology: Moiré patterns can be used for precision measurements, especially for detecting small displacements or strains in materials.
- Art and Design: Artists sometimes intentionally use Moiré patterns to create optical illusions or dynamic visuals.
- Textile Industry: Fabric designers are aware of Moiré patterns and can either avoid them or use them to create interesting visual effects.
- Image Processing: Moiré patterns are considered noise in digital imaging, and algorithms are designed to detect and remove them.
- Structural Analysis: Engineers use Moiré patterns to study strain in materials by overlaying grids on objects and analyzing how the patterns change under stress.
7. Example of Moiré Pattern in Imaging
Let’s consider an example where a digital camera takes a picture of a patterned object, such as a tightly woven fabric.
- The fabric has a periodic pattern of lines spaced 0.1 mm apart.
- The camera sensor has a pixel grid with a spacing of 0.11 mm (slightly larger than the fabric’s line spacing).
- The result is a visible Moiré pattern, where the interference between the fabric lines and the sensor’s pixel grid creates a ripple-like distortion.
The 2-D Discrete Fourier Transform and Its Inverse
The 2-D Discrete Fourier Transform (DFT) is a crucial mathematical tool used in image processing and signal processing to analyze frequency content in two-dimensional data, such as images. It transforms a 2D signal (like an image) from the spatial domain into the frequency domain. The inverse operation, the Inverse 2-D DFT, allows us to convert the signal back from the frequency domain to the spatial domain.
This transformation reveals the frequency components present in the image, which is essential for tasks such as filtering, image compression, and enhancement.
1. The 2-D Discrete Fourier Transform (DFT)
The 2-D DFT takes a 2D array (typically representing an image) and transforms it into a 2D array in the frequency domain. Each value in the transformed array represents the magnitude and phase of a specific frequency component in the image.
Mathematical Formula of the 2-D DFT
Let be a 2D image or signal of size . The 2-D DFT of this image is given by:
Where:
- is the intensity of the pixel at position in the spatial domain.
- is the value of the frequency domain representation at frequency coordinates .
- and are the dimensions of the image.
- is the imaginary unit .
- The exponential term represents the complex sinusoidal basis functions for the transformation.
Explanation:
- and are the frequencies in the horizontal and vertical directions, respectively.
- The sum over all pixels computes the contribution of each pixel in the spatial domain to each frequency component in the frequency domain.
- The resulting values are complex numbers that encode both magnitude (how strong the frequency is) and phase (the shift or alignment of the frequency).
Magnitude and Phase:
Magnitude : Represents the strength of the frequency component.
Phase : Represents the shift or displacement of the frequency component.
2. The Inverse 2-D Discrete Fourier Transform (IDFT)
The Inverse 2-D DFT is used to convert the data from the frequency domain back to the spatial domain, reconstructing the original image from its frequency components.
Mathematical Formula of the Inverse 2-D DFT
The Inverse 2-D DFT is given by:
Where:
- is the frequency domain value at .
- is the reconstructed pixel value at in the spatial domain.
- The exponential term is now positive, reversing the transformation from the frequency domain back to the spatial domain.
- The factor normalizes the result.
Explanation:
- The Inverse DFT essentially sums the contributions of all frequency components (with their respective magnitudes and phases) to reconstruct the image in the spatial domain.
- The complex exponential functions in the summation act as the inverse basis functions, converting frequency information back to spatial information.
3. Understanding the Frequency Domain
In the frequency domain, the low-frequency components (i.e., large, slow changes in pixel intensity) are located near the center of the transformed image, while the high-frequency components (i.e., rapid, small changes in intensity such as edges or textures) are located towards the edges.
- Low frequencies correspond to smooth variations in intensity over large areas.
- High frequencies correspond to fine details like edges and sharp transitions.
Visual Representation of Frequency Components:
- In an image transformed by the 2-D DFT, each point in the frequency domain represents a particular sinusoidal component of the image:
- The magnitude at each point represents how much of that frequency is present in the image.
- The phase at each point tells you how that frequency is aligned in the image.
4. Example of the 2-D DFT and IDFT
Consider an example of a simple 4×4 image:
Original Image :
Step 1: Compute the 2-D DFT
Using the 2-D DFT formula, we compute the frequency domain representation. In this small example, we won’t perform the full calculations (since it’s complex), but we can describe the result conceptually:
- The low-frequency components (smooth parts of the image) will be near the center.
- High-frequency components (sharp transitions, like the alternating 0s and 1s) will appear at higher values of and , near the corners.
Step 2: Frequency Domain Representation
For this 4×4 image, the frequency domain representation might look like:
- The high magnitude values (like 8) represent strong frequencies in the image, and negative values (like -4) represent phase shifts.
- The zeros indicate that certain frequencies are not present in the image.
Step 3: Compute the Inverse 2-D DFT
Using the Inverse 2-D DFT, we can convert back into the spatial domain to reconstruct the original image:
The result will be the original image :
Thus, the Inverse DFT has successfully reconstructed the original image from its frequency components.
5. Applications of the 2-D DFT
The 2-D DFT and its inverse are widely used in several applications, especially in image processing:
5.1 Image Filtering
- Low-pass filtering: Remove high-frequency components to blur the image or reduce noise.
- High-pass filtering: Retain only high-frequency components to enhance edges and sharp details.
5.2 Image Compression
Many image compression algorithms, like JPEG, rely on the 2-D DFT. By transforming the image into the frequency domain, we can:
- Discard insignificant frequency components (usually the high-frequency ones), leading to efficient compression.
- Retain the most significant low-frequency components to maintain image quality.
5.3 Pattern Recognition
The frequency domain representation can be used to detect repeating patterns or textures in images by analyzing specific frequency components.
References
- Stewart, J. (2015). Calculus: Early Transcendentals (8th ed.). Cengage Learning.
- Thomas, G. B., Weir, M. D., & Hass, J. (2018). Thomas’ Calculus (14th ed.). Pearson.
- Strang, G. (2016). Calculus (Vol. 1). Wellesley-Cambridge Press.
- Rogawski, J., & Adams, C. (2019). Calculus: Early Transcendentals (4th ed.). W. H. Freeman.
