Gray-Scale Morphology

by

Gray-scale morphology is a set of image processing techniques that operates on gray-scale images using mathematical morphological operations. It’s particularly useful for enhancing image details, removing noise, and preparing images for analysis by focusing on their structure. Unlike binary morphology (which is for binary images), gray-scale morphology considers the intensity of pixels, making it suitable for continuous-tone images.

Nonflat and flat structuring elements, and corresponding horizontal intensity profiles through their center. All examples in this section are based on flat SEs
A
B
C
(a) A gray-scale X-ray image of size (b) Erosion using a flat disk SE with a radius of two pixels. (c) Dilation using the same SE. (Original image courtesy of Lixi, Inc.)

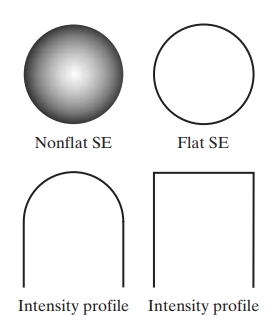
1. Structuring Element in Gray-Scale Morphology

In gray-scale morphology, a structuring element (SE) is a small matrix that defines the neighborhood over which morphological operations are performed. This element has values that represent pixel intensities, and it is used to probe and interact with the pixels in the image. Typical SEs are small matrices (e.g., 3×3, 5×5) that have various shapes such as a flat disk, square, or line.

2. Basic Operations in Gray-Scale Morphology

Gray-scale morphological operations include erosion, dilation, opening, and closing. Let’s break down each operation with its mathematical concept and an example.

A. Erosion (Minimization)

Definition: Gray-scale erosion of an image ff by a structuring element bb is the process of moving bb over each pixel in ff and replacing the pixel’s value with the minimum value covered by bb at that location.

Mathematical Concept:

(f⊖b)(x,y)=min⁡{f(x+s,y+t)−b(s,t)∣(s,t)∈domain of b}(f \ominus b)(x, y) = \min \{ f(x + s, y + t) – b(s, t) \mid (s, t) \in \text{domain of } b \}

where:

  • f(x,y)f(x, y) is the gray-scale image.
  • b(s,t)b(s, t) is the structuring element.

Example: Suppose we have a 3×3 region of an image:

f=[120125130128135138132137140]f = \begin{bmatrix} 120 & 125 & 130 \\ 128 & 135 & 138 \\ 132 & 137 & 140 \end{bmatrix}

If the structuring element bb is flat (all elements zero), erosion will take the minimum of each neighborhood. For a flat 3×3 SE, the output will be the minimum of all values in each 3×3 neighborhood around each pixel.

B. Dilation (Maximization)

Definition: Gray-scale dilation of an image ff by a structuring element bb is the process of moving bb over each pixel in ff and replacing the pixel’s value with the maximum value covered by bb at that location.

Mathematical Concept:

(f⊕b)(x,y)=max⁡{f(x−s,y−t)+b(s,t)∣(s,t)∈domain of b}(f \oplus b)(x, y) = \max \{ f(x – s, y – t) + b(s, t) \mid (s, t) \in \text{domain of } b \}

Example: Using the same 3×3 image ff from the previous example and a flat 3×3 SE, the output of dilation will be the maximum value in each 3×3 neighborhood around each pixel.

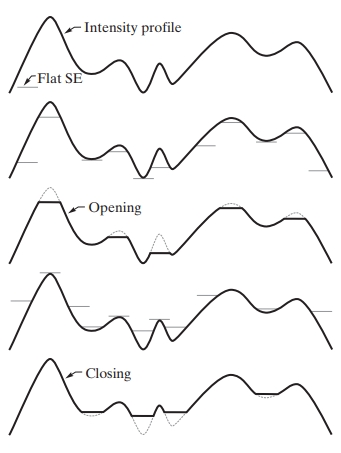
C. Opening

Definition: Opening is a two-step process: it first applies erosion, then applies dilation. Opening smooths out edges, removes small objects, and disconnects thin structures.

Mathematical Concept:

f∘b=(f⊖b)⊕bf \circ b = (f \ominus b) \oplus b

Example: For the image ff and a 3×3 SE, opening will erode ff, which reduces intensity values in bright regions, followed by dilation to restore some of the structure.

D. Closing

Definition: Closing is also a two-step process: it first applies dilation, then erosion. It is useful for closing small holes and connecting narrow breaks in an image.

Mathematical Concept:

f∙b=(f⊕b)⊖bf \bullet b = (f \oplus b) \ominus b

Example: For the image ff, closing will first dilate ff, which enhances bright areas, followed by erosion to smooth out the result.

A: Opening and closing in one dimension: (a) Original 1-D signal. (b) Flat structuring element pushed up underneath the signal. (c) Opening. (d) Flat structuring element pushed down along the top of the signal. (e) Closing.
B: (a) A gray-scale X-ray image of size (b) Erosion using a flat disk SE with a radius of two pixels. (c) Dilation using the same SE. (Original image courtesy of Lixi, Inc.)
C: (a) Image of the Cygnus Loop supernova, taken in the X-ray band by NASA’s Hubble Telescope.
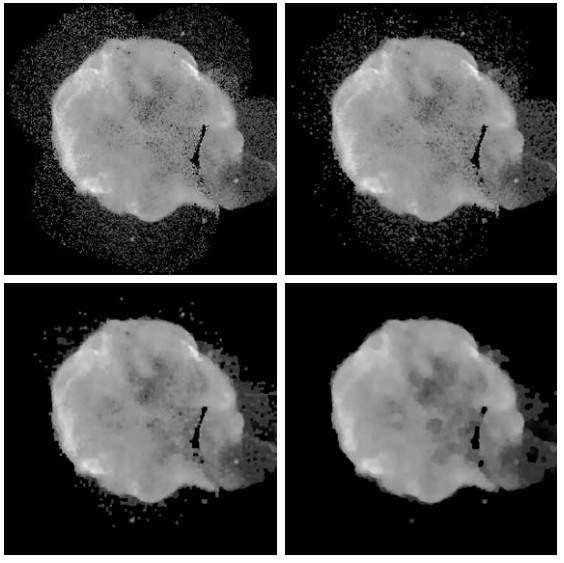
(b)–(d) Results of performing opening and closing sequences on the original image using disk-shaped structuring elements with radii of 1, 3, and 5 pixels, respectively.
(Original image courtesy of NASA.)
Image size: 566 x 566 pixels.
D: (a) Image of a head CT scan. (b) Dilation. (c) Erosion. (d) Morphological gradient, computed as the difference between (b) and (c). (Original image courtesy of Dr. David R. Pickens, Vanderbilt University.) Image size: 512 x 512 pixels.
E: Using the top-hat transformation for shading correction: (a) Original image of size 600 x 600 pixels. (b) Thresholded image. (c) Image opened using a disk-shaped structuring element (SE) with a radius of 40 pixels. (d) Top-hat transformation (the original image minus its opening). (e) Thresholded top-hat image.
F: Differences in surface area as a function of SE disk radius, The two peaks are indicative of two dominant particle sizes in the image

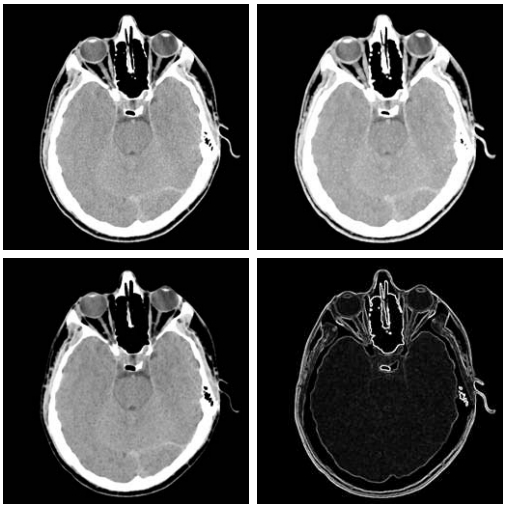
3. Some Basic Gray-Scale Morphological Algorithms

Gray-scale morphology can be applied to create specific algorithms useful in image processing.

  • Top-Hat Transformation: Highlights small structures that are lighter than their surroundings. Top-Hat=f−(f∘b)\text{Top-Hat} = f – (f \circ b)
  • Bottom-Hat Transformation: Highlights small structures that are darker than their surroundings. Bottom-Hat=(f∙b)−f\text{Bottom-Hat} = (f \bullet b) – f

Example: Using the top-hat transformation, we can detect bright spots in a gray-scale image, which is particularly useful in astronomy to detect stars against a darker sky background.

4. Gray-Scale Morphological Reconstruction

Gray-scale morphological reconstruction is a technique that involves reconstructing an image by iteratively dilating a “marker” image until it fits within the boundaries of another “mask” image. Reconstruction is effective in removing undesired artifacts without distorting the shape of objects.

  • Erosion-Based Reconstruction: It starts from a marker image and iteratively applies erosion until the marker conforms to the mask.
  • Dilation-Based Reconstruction: It starts from a marker and applies dilation until it conforms to the mask.

Mathematical Concept: Let ff be the mask image and gg the marker image. The reconstruction of gg from ff by dilation, denoted Rf(g)R_f(g), is obtained by:

Rf(g)=lim⁡k→∞(g⊕f)kR_f(g) = \lim_{k \to \infty} (g \oplus f)^k

Example: If we want to highlight regions that have bright cores in an image (e.g., cells in a microscopy image), we can use a gray-scale morphological reconstruction by dilation. The core regions (marker image) are iteratively dilated to match the boundary defined by the mask image (original image).

Summary of Operations

OperationDescriptionMathematical Representation
ErosionReduces brightness in bright regionsf⊖bf \ominus b
DilationEnhances brightness in bright regionsf⊕bf \oplus b
OpeningRemoves small bright areasf∘b=(f⊖b)⊕bf \circ b = (f \ominus b) \oplus b
ClosingFills small dark areasf∙b=(f⊕b)⊖bf \bullet b = (f \oplus b) \ominus b
Top-HatDetects small bright structuresf−(f∘b)f – (f \circ b)
Bottom-HatDetects small dark structures(f∙b)−f(f \bullet b) – f
ReconstructionRecovers specific shapes in an imageRf(g)=lim⁡k→∞(g⊕f)kR_f(g) = \lim_{k \to \infty} (g \oplus f)^k

Each of these techniques is essential in preprocessing and analyzing gray-scale images, especially in fields like medical imaging, industrial inspection, and remote sensing, where structural details in continuous-tone images are key to analysis.

References

  1. Books:
    • Gonzalez, R. C., & Woods, R. E. (2018). Digital Image Processing (4th Edition). Pearson.
    • Haralick, R. M., & Shapiro, L. G. (1992). Computer and Robot Vision, Vol. 1. Addison-Wesley.
    • Serra, J. (1983). Image Analysis and Mathematical Morphology. Academic Press. Jean Serra is one of the founders of mathematical morphology
  2. Research Articles:
    • Vincent, L., & Soille, P. (1991). Watersheds in Digital Spaces: An Efficient Algorithm Based on Immersion Simulations. IEEE Transactions on Pattern Analysis and Machine Intelligence, 13(6), 583–598.
    • Soille, P. (2003). Morphological Image Analysis
  3. Online Resources:
    • MathWorks Documentation on Morphological Operations
    • OpenCV Documentation on Morphological Operations

Leave a Comment