Image Pyramids

Gaussian Pyramid

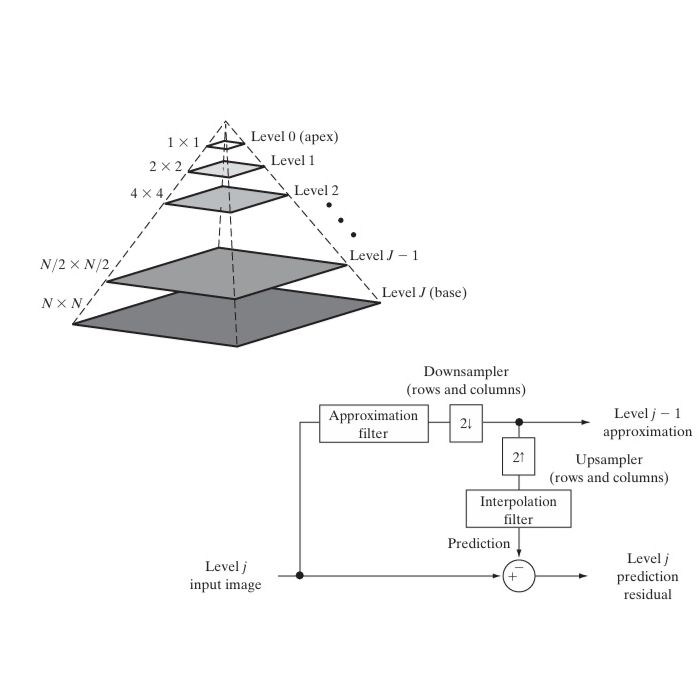
A Gaussian pyramid is constructed by repeatedly applying a Gaussian filter and downsampling the image. The process consists of generating successively smaller and smoother versions of the original image by applying a low-pass filter (Gaussian filter) and downsampling (reducing the image size).

Mathematical Formulation: Given an image $I_0$, the process to create a Gaussian pyramid can be written as follows:

1. Apply a Gaussian filter:

   $$G(x, y) = \frac{1}{2\pi\sigma^2} \exp\left(-\frac{x^2 + y^2}{2\sigma^2}\right)$$

   where $\sigma$ controls the amount of smoothing, and $(x, y)$ represent the pixel coordinates.

2. Downsample the image by a factor of 2:

   $$I_{n+1}(x, y) = \text{Downsample}\left(G(x, y) * I_n(x, y)\right)$$

   where $*$ denotes the convolution operation, and $I_{n+1}$ is the downsampled version of the image at level $n+1$.

This process is repeated for multiple levels to build the pyramid. Each subsequent level contains an image of reduced resolution, but retains key structural features of the original.

2. Laplacian Pyramid

A Laplacian pyramid is constructed by taking the difference between consecutive levels of the Gaussian pyramid. This allows us to capture the high-frequency components or details between different scales.

Mathematical Formulation: To construct the Laplacian pyramid, we need the Gaussian pyramid first. Let $I_n$ be the image at level $n$ in the Gaussian pyramid. The Laplacian pyramid $L_n$ is calculated as follows:

1. Upsample the image from level $n+1$:

   $$I^{\uparrow}_{n+1}(x, y) = \text{Upsample}(I_{n+1}(x, y))$$

2. Compute the difference between the Gaussian image at level $n$ and the upsampled image:

   $$L_n(x, y) = I_n(x, y) – I^{\uparrow}_{n+1}(x, y)$$

This difference captures the details (high-frequency information) between the two levels. The process is repeated for each level, creating a Laplacian pyramid that represents the image’s fine details at multiple scales.

Example Using an Input Image

Step-by-Step Example: Gaussian and Laplacian Pyramid Construction

Consider a grayscale image $I_0$ of size 512×512 pixels. We will construct both the Gaussian and Laplacian pyramids.

1. Gaussian Pyramid Construction:

   • Level 0 (Original Image): $I_0$ is the original image.
   • Level 1: Apply Gaussian smoothing and downsample $I_0$ to obtain $I_1$ of size 256×256 pixels.
   • Level 2: Apply Gaussian smoothing to $I_1$ and downsample to obtain $I_2$ of size 128×128 pixels.
   • Level 3: Repeat the process to obtain $I_3$ of size 64×64 pixels.
   • Continue until the desired number of levels is reached.

2. Laplacian Pyramid Construction:

   • Level 3 (Laplacian): Compute the difference between $I_3$ and the upsampled version of $I_4$ (size 64×64) to get the Laplacian image $L_3$.
   • Level 2 (Laplacian): Compute the difference between $I_2$ and the upsampled version of $I_3$ (size 128×128).
   • Level 1 (Laplacian): Similarly, compute the difference between $I_1$ and the upsampled version of $I_2$ (size 256×256).

Each level of the Laplacian pyramid will represent the image details at that specific resolution.

Applications of Image Pyramids

1. Image Compression: Laplacian pyramids are used for compact image representations. The high-frequency details stored in the Laplacian pyramid levels can be quantized and compressed more efficiently than storing the full-resolution image.

2. Object Detection: In computer vision, objects can appear at different scales in an image. Gaussian pyramids allow detection algorithms (such as the Scale-Invariant Feature Transform, or SIFT) to detect objects at different scales by analyzing the image at each pyramid level.

3. Image Blending: In tasks such as image stitching or blending, pyramids are used to smoothly blend two images by merging them at different levels of resolution. This results in seamless transitions between images.

Multiresolution and Wavelet Processing

Wavelets are another important concept closely related to image pyramids. They provide a powerful framework for analyzing an image at different resolutions. A wavelet transform decomposes an image into sub-bands, similar to the decomposition in a Laplacian pyramid. The advantage of wavelets is their ability to capture both frequency and spatial information, making them highly effective for image compression, denoising, and feature extraction.

Conclusion

Image pyramids, whether Gaussian or Laplacian, are essential tools in modern image processing. They provide efficient multi-resolution representations of images, making them useful in tasks such as compression, object detection, and blending. Understanding the underlying mathematical concepts, such as Gaussian filtering, downsampling, upsampling, and the construction of Laplacian pyramids, allows for more advanced applications in fields like computer vision and image analysis.

This comprehensive approach to multi-resolution processing also ties into the theory of wavelets, opening up further opportunities for research and application.

References

1. Burt, P., & Adelson, E. H. (1983). The Laplacian Pyramid as a Compact Image Code. IEEE Transactions on Communications, 31(4), 532–540.
2. Mallat, S. (1989). A Theory for Multiresolution Signal Decomposition: The Wavelet Representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11(7), 674–693.
3. Lindeberg, T. (1994). Scale-space theory: A basic tool for analyzing structures at different scales. Journal of Applied Statistics, 21(2), 224–270.
4. Szeliski, R. (2010). Computer Vision: Algorithms and Applications. Springer.
5. Lowe, D. G. (2004). Distinctive Image Features from Scale-Invariant Keypoints. International Journal of Computer Vision, 60(2), 91–110.
6. Gonzalez, R. C., & Woods, R. E. (2007). Digital Image Processing (3rd ed.). Pearson Prentice Hall.
7. Porikli, F., Meer, P., & Tuzel, O. (2006). Fast and Robust Multiresolution Histogram Tracking. IEEE Transactions on Pattern Analysis and Machine Intelligence, 30(6), 1024–1035.