The main causes of noise in digital images happen during the process of capturing or sending the image. Imaging sensors can be affected by various things, like the environment when the picture is taken or the quality of the sensors themselves. For example, when using a CCD camera, the amount of light and the sensor’s temperature play big roles in how much noise appears in the image.
When images are sent from one place to another, noise can occur due to interference in the transmission. For instance, if an image is sent over a wireless network, it could be distorted by things like lightning or other weather conditions.
A Model of the Image Degradation/Restoration Process
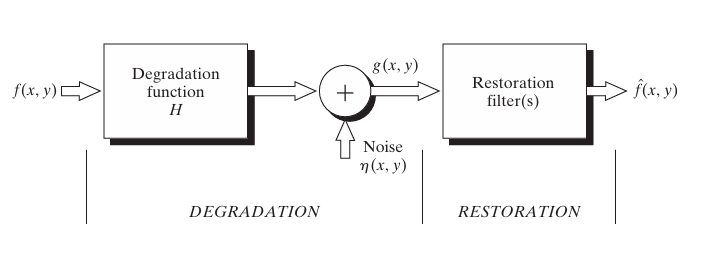
In image processing, images are often degraded due to various factors such as noise, motion blur, or sensor imperfections. The Image Degradation/Restoration Process models this degradation mathematically and provides techniques to recover the original image. This process is fundamental in applications like medical imaging, satellite imagery, and photography, where images need to be restored to a clearer form.
1. Image Degradation Model
The degradation process of an image can be expressed mathematically as a combination of the true (original) image, some degrading function, and additive noise. The general form of this model is:
Where:
- is the observed degraded image.
- is the original (ideal) image.
- is the degradation function (also called the point spread function, or PSF), which models how the image gets blurred or distorted. It might represent, for instance, camera motion or atmospheric distortion.
- denotes convolution.
- is the additive noise, representing random disturbances like sensor noise or transmission errors.
This model assumes that the degradation process can be modeled as convolution (linear operation) followed by additive noise (nonlinear operation).
2. Image Restoration Model
The goal of the image restoration process is to estimate the original image given the degraded image , the degradation function , and the characteristics of the noise . Mathematically, the restoration process can be seen as solving the inverse problem of the degradation model.
In the frequency domain, the degradation model becomes simpler using Fourier transforms. Taking the 2D Fourier transform of the degradation model:
Where:
- , , , and are the Fourier transforms of the degraded image, the degradation function, the original image, and the noise, respectively.
- represent the frequency variables.
In this domain, convolution becomes multiplication, which simplifies many restoration methods.
Restoration Techniques:
Several approaches can be applied to restore the degraded image. Below are the most common methods:
3. Inverse Filtering
Inverse filtering is the most straightforward approach to image restoration. In the frequency domain, the original image can be estimated as:
This means the degraded image is divided by the degradation function in the frequency domain, thereby “undoing” the effects of the degradation function.
Challenges with Inverse Filtering:
- Noise amplification: If is close to zero for some frequencies, the result can be noisy or unstable.
- Not robust to noise: Since noise is always present in practical situations, this method might amplify noise in the restored image.
Example: Consider an image that has been blurred due to motion. If the motion blur can be modeled with a known function , we can take the Fourier transform of the blurred image, apply inverse filtering, and recover an approximation of the original image.
4. Wiener Filtering
Wiener filtering is an optimal approach to image restoration, which minimizes the mean square error between the estimated image and the true image. It is particularly effective when noise is present. The Wiener filter in the frequency domain is given by:
Where:
- is the complex conjugate of the degradation function.
- is the power spectral density of the noise.
- is the power spectral density of the original image.
- is the squared magnitude of .
The Wiener filter accounts for both the degradation and the presence of noise, balancing the effects of inverse filtering and noise suppression.
Advantages of Wiener Filtering:
- It handles noise optimally by considering both the degradation function and noise statistics.
- The filter does not amplify noise as much as inverse filtering.
Example: A medical image obtained through an MRI scan might suffer from noise due to low signal strength and equipment limitations. Applying the Wiener filter, where both the noise and degradation function are known or estimated, helps in restoring a cleaner, more accurate image.
5. Regularized Restoration
Another approach to handle image degradation and noise is through regularization. This method involves formulating the restoration as an optimization problem where a regularization term is added to enforce smoothness or other constraints on the restored image.
The restoration problem can be written as:
Where:
- is the data fidelity term, ensuring that the restored image matches the observed data.
- is the regularization parameter, controlling the trade-off between the data fidelity and smoothness of the solution.
- is the regularization term, where might represent the derivative of the image, enforcing smoothness (i.e., penalizing large variations).
Advantages of Regularized Restoration:
- It helps recover stable solutions in cases where inverse filtering would fail due to noise or when the degradation function is ill-conditioned.
- Different types of regularization can enforce specific prior knowledge about the image, such as smoothness, edges, or sparsity.
Example: Consider restoring an astronomical image where details like stars or distant galaxies might be blurred. Regularized restoration can enforce smoothness to remove noise while preserving important structures in the image.
6. Constrained Least Squares Filtering
This technique is a type of regularization method where the solution is found by minimizing the squared error between the observed and restored images, subject to a smoothness constraint. It can be formulated as:
Where:
- is the Fourier transform of a Laplacian operator that enforces smoothness.
- is a regularization parameter that controls the trade-off between fitting the degraded image and enforcing smoothness.
Advantages:
- It combines noise reduction with image restoration.
- Can be adapted for different types of images and degradation functions by modifying the regularization term.
Example: An image captured by a drone flying at high altitude might suffer from atmospheric blur and noise. Constrained least squares filtering, using a proper degradation model and regularization, can help in restoring the image while reducing noise.
7. Blind Deconvolution
In many practical situations, the degradation function is unknown. Blind deconvolution refers to restoring the image while simultaneously estimating the degradation function. This is a highly complex task but essential in cases where the point spread function (PSF) cannot be measured directly.
Blind deconvolution can be tackled using iterative algorithms that alternately estimate the image and the degradation function. An example of such an algorithm is the Richardson-Lucy deconvolution.
Advantages of Blind Deconvolution:
- It works even when the exact degradation model is unknown.
- Effective in restoring images affected by unknown blur, such as motion blur or atmospheric distortion.
Example: A photograph taken with a moving camera might be blurred, and the exact nature of the blur might not be known. Blind deconvolution can help recover both the original image and the blur function, improving the overall image quality.
Spatial and Frequency Properties of Noise
Noise in digital images can be defined by its spatial characteristics and whether it is correlated with the image. The frequency properties of noise are understood in the Fourier sense rather than in terms of electromagnetic frequencies. When the Fourier spectrum of noise is constant, it is referred to as white noise, a term borrowed from the concept of white light containing all visible frequencies in equal amounts. Typically, noise is considered independent of spatial coordinates and uncorrelated with the image, meaning there is no relationship between pixel values and the noise. However, in cases like quantum-limited imaging (such as X-rays and nuclear medicine), these assumptions may not fully apply.
Some Important Noise Probability Density Functions
In digital signal processing and image analysis, noise plays a critical role in determining the quality of signals and images. Noise refers to unwanted random variations that interfere with the original signal, often making it harder to analyze or interpret data accurately. Understanding the behavior of noise is essential for improving signal processing techniques and enhancing image clarity.
One way to describe noise is through probability density functions (PDFs), which model how noise is distributed across different values. These PDFs help in predicting the likelihood of specific noise levels occurring in a signal. Different types of noise exhibit unique characteristics, and each type can be represented by a distinct probability density function.
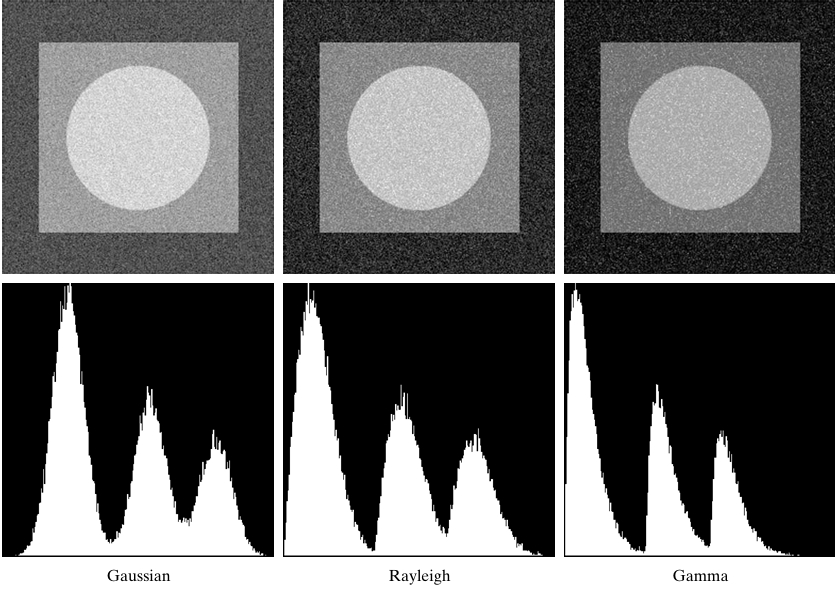
Gaussian noise
Gaussian noise, also known as additive white Gaussian noise (AWGN), is a type of random noise characterized by a normal distribution. This noise is common in signal processing, image processing, and communication systems, where it introduces random fluctuations to the data.
Mathematical Model of Gaussian Noise
Gaussian noise is typically modeled as:
In this model:
- is the noise at a pixel or data point .
- represents a normal distribution with mean and variance .
- The mean represents the average value of the noise (commonly set to zero).
- The variance measures how widely the noise values spread around the mean.
Gaussian Distribution
The probability of different noise values is described by the Gaussian (or normal) distribution function:
Where:
- is the probability of the noise value .
- is the mean of the noise, which is often zero.
- is the standard deviation, related to the variance ().
- is the exponential function.
This distribution indicates that noise values closer to the mean are more likely, while extreme values are rare.
Example
Suppose you have an image with a pixel intensity value of 120. If Gaussian noise with a mean and a standard deviation is applied, a random noise value could be drawn from the distribution. For instance, the sampled noise might be . In this case, the new pixel value would be:
Here, the noise has slightly reduced the pixel intensity.
Effects in Images
When Gaussian noise is added to an image, it appears as grainy or speckled variations across the pixels. These fluctuations are especially noticeable in uniform areas or low-light regions. The strength of the noise depends on the variance ; higher variance leads to more visible noise.
Applications of Gaussian Noise
Gaussian noise is commonly used to simulate real-world conditions in systems like:
- Communication Systems: To test the reliability of signal transmission under noisy conditions.
- Image Processing: To evaluate how well algorithms can remove or handle noise.
By adding Gaussian noise artificially, engineers and researchers can assess how well systems or algorithms perform in noisy environments.
Rayleigh noise
Rayleigh noise is a type of statistical noise that appears in systems where signals experience random scattering, such as in radar, wireless communications, and certain image processing applications. It arises when the magnitude of a vector, composed of two orthogonal components that follow normal distributions, is observed. This type of noise is particularly useful in modeling environments where signals encounter multiple reflections or scatterings before reaching the receiver.
Mathematical Definition:
The probability density function (PDF) of Rayleigh noise is described by the following equation:
Where:
- is the noise amplitude (a non-negative random variable).
- is the scale parameter that determines the spread of the distribution.
- The PDF is defined only for , meaning Rayleigh noise takes positive values.
The distribution starts at zero, increases to a peak at , and then decays exponentially for larger values of .
Properties of Rayleigh Noise:
- Asymmetric Distribution: Unlike Gaussian noise, which is symmetric around its mean, Rayleigh noise has a skewed distribution that only allows positive values.
- Defined by One Parameter: The distribution’s shape is controlled solely by the parameter , which represents the scale of the noise.
- Common in Scattering Environments: Rayleigh noise occurs in situations where a signal is scattered or reflected, such as in wireless channels or radar systems.
Example:
Suppose Rayleigh noise follows a distribution with . The probability density function is:
To calculate the probability density at :
This shows that the likelihood of the noise having an amplitude of 4 is about 0.183.
Applications of Rayleigh Noise:
Wireless Communications: Rayleigh noise is commonly used to model fading in wireless communication channels, especially in urban environments where multiple signal paths arise due to reflection and scattering. For instance, when a mobile phone receives signals, some of the signal paths are longer due to reflections from buildings, causing random variations in the signal strength. These variations follow the Rayleigh distribution.
Radar Systems: Rayleigh noise appears in radar systems when reflected signals scatter off multiple objects before returning to the radar receiver. In such scenarios, the strength of the reflected signal varies unpredictably, and the Rayleigh distribution provides an accurate model for this randomness.
Image Processing: In medical imaging, such as ultrasound, Rayleigh noise models random variations in pixel intensity caused by scattering within tissues. The skewed nature of the distribution makes it an ideal model for noise in these images.
Noise Reduction Techniques:
Median Filtering: A commonly used method to reduce Rayleigh noise in images, median filtering smooths the noise while preserving edges. It works by replacing each pixel value with the median value of its neighboring pixels.
Adaptive Filters: In wireless communications, adaptive filters can be used to reduce Rayleigh noise by adjusting to the dynamic variations in the noise pattern over time. These filters help in minimizing signal distortion caused by fading.
Wavelet Denoising: This technique decomposes the signal into wavelet components and applies thresholding to remove noise. It is especially effective in cases where Rayleigh noise affects fine details, such as in radar and ultrasound images.
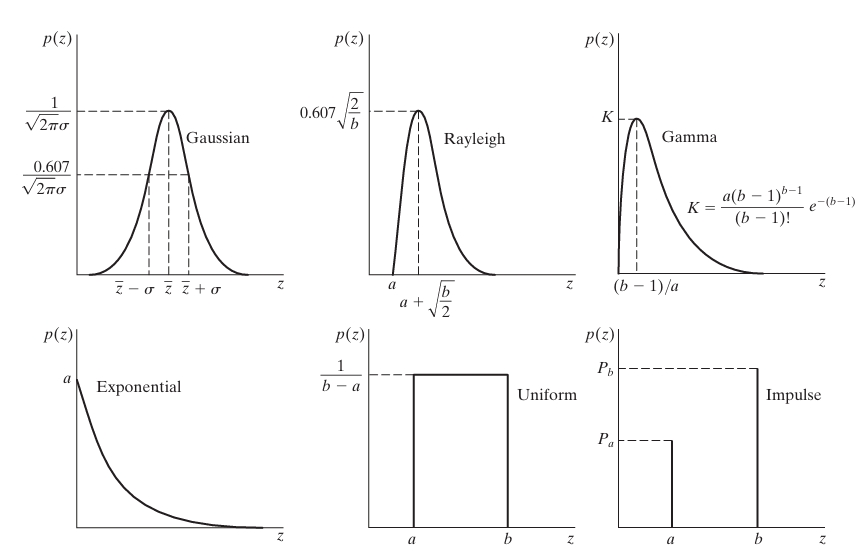
Erlang (gamma) noise
Erlang noise, also known as Gamma noise, follows the Gamma distribution. It is commonly used in modeling random events, such as packet arrivals in communication systems or waiting times in queueing systems. This type of noise is important in scenarios where events occur in groups or phases, and the time between events is random.
The Gamma distribution has the following probability density function (PDF):
Where:
- is the value of the noise (and must be positive).
- is the shape parameter, which is an integer for Erlang noise.
- is the scale parameter, determining the spread of the noise values.
- is the Gamma function, which generalizes the factorial. For integer , .
The Erlang distribution is a specific case of the Gamma distribution where the shape parameter is a positive integer. It is often used to describe the sum of independent exponential random variables, representing the time until the occurrence of events.
The mean and variance of the Erlang distribution are:
This shows that the mean is proportional to both the number of events () and the average time between events (), while the variance increases with both.
Example
Suppose you are modeling the time between customer arrivals at a service center. If the shape parameter and the average time between arrivals minutes, the mean arrival time is:
The variance of the arrival times would be:
This example illustrates how Erlang noise can model systems where multiple events occur randomly over time.
Applications
Erlang (Gamma) noise is used in several areas:
- Communication systems: It can model packet arrival times where multiple packets are sent in bursts, following a random process.
- Queueing theory: In systems where customers or tasks arrive at random intervals, the waiting times between these events are often modeled with Erlang distributions.
- Wireless communications: In some cases, the variability in signal strength caused by fading can be modeled with the Gamma distribution, especially when multiple independent paths are involved.
Visual Effects in Systems
When a system is affected by Erlang noise, the timing or intensity of the events in the system fluctuates in a structured but random manner. For example, in a network, data packets might not arrive at uniform intervals but instead come in bursts, creating variability in processing times.
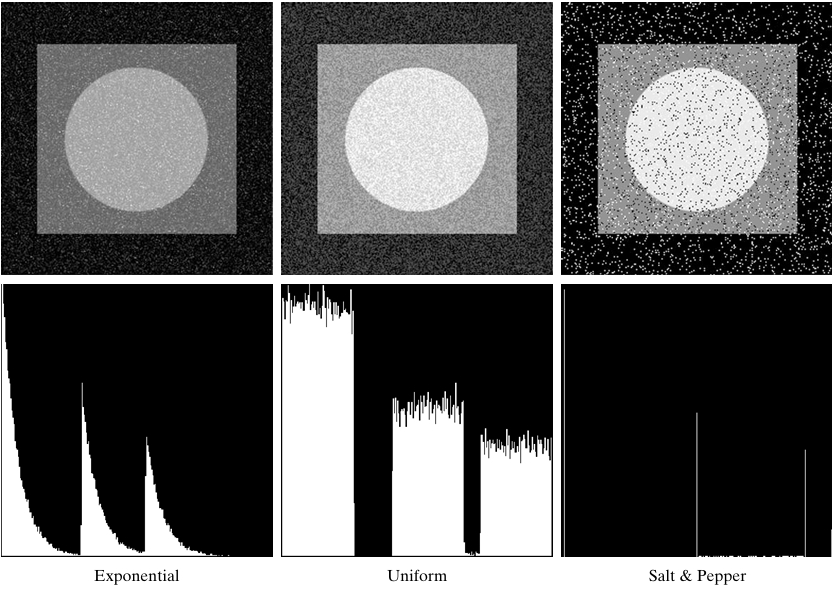
Exponential noise
Exponential noise refers to random variations that follow an exponential distribution. This distribution is used in scenarios where events occur continuously and independently, often in communication systems or processes that involve waiting times.
Mathematical Concept of Exponential Noise:
The probability density function (PDF) of exponential noise is expressed as:
In this equation:
- is the rate parameter, a positive constant that determines the distribution’s shape. It controls how fast the probability decays as increases.
- is the noise value, representing the random variable.
- is the base of the natural logarithm, approximately 2.71828.
The rate parameter affects the nature of the noise:
- A larger results in most of the noise values being closer to zero (small noise).
- A smaller means larger noise values are more likely.
Properties:
- The mean (average value) of the noise is .
- The variance, which represents the spread or variability of the noise, is .
Example:
Consider a situation where you are modeling the time between failures of a machine, with an average time of 4 hours between failures. Here, the rate parameter is , since .
The probability that the machine will not fail within hours is given by:
For instance:
- If hours, the probability that the machine does not fail within 3 hours is:
This means there’s about a 47.24% chance that the machine will run without failure for at least 3 hours.
- If hours, the probability becomes:
Thus, there’s about a 22.31% chance the machine will last 6 hours without failure.
Applications:
Exponential noise is applied in many fields, including:
- Signal Processing: Modeling random noise in communication systems.
- Reliability Engineering: Estimating the time between failures in machines or systems.
- Queueing Theory: Predicting the time between arrivals of customers or events in a service system, such as the time between phone calls in a call center.
In general, exponential noise is associated with processes where events happen randomly but at a steady average rate.
Uniform noise
Uniform noise refers to a type of noise where each value within a specific range is equally likely to occur. This means that every possible value in that range has the same probability of being selected. It is a simple form of random noise, often used in simulations, testing, and various signal processing applications.
Mathematically, uniform noise is described by a uniform distribution, typically over an interval , where and represent the minimum and maximum values of the noise. The probability of any value occurring within this range is the same.
The probability density function (PDF) for uniform noise is:
Where:
- is the lower bound (minimum value) of the noise.
- is the upper bound (maximum value) of the noise.
- is the noise value.
- represents the constant probability for any value within the range.
In this formula, the probability is spread evenly across the interval , meaning that any noise value within this range is equally likely to occur.
Mean and Variance of Uniform Noise:
The mean (or expected value) of uniform noise is the midpoint of the range , calculated as:
The variance, which measures how much the noise values differ from the mean, is given by:
This variance represents how spread out the noise values are. A larger interval results in a higher variance, meaning the noise values are more spread.
Example of Uniform Noise:
Consider a scenario where we are generating random numbers between 2 and 8. This can be modeled using uniform noise over the interval .
The mean of the noise is:
So, the average value of the noise is 5.
The variance is:
This means the noise values are somewhat spread around the mean.
In this case, any value between 2 and 8 has the same probability of being selected, making the distribution “uniform” across the interval.
Applications of Uniform Noise:
- Simulations: Uniform noise is used in simulations when generating random events or outcomes where all possibilities within a range should be equally likely.
- Image Processing: It is used for adding artificial noise to images for testing or analysis.
- Signal Processing: Uniform noise is useful for testing systems and algorithms, as it provides an evenly distributed set of random values within a specified range.
This type of noise is ideal when you need simple, predictable randomness with equal probabilities across a range of values.
Periodic Noise
Periodic noise is a type of noise that occurs in regular, repeating patterns over time or space. This noise typically originates from external interference, such as mechanical vibrations or electrical disturbances. It is often found in both signal and image processing, where it can degrade the quality of the data being analyzed.
Mathematically, periodic noise can be represented using a sinusoidal function, which describes its repeating behavior. A simple expression for periodic noise is:
In this equation:
- is the amplitude, representing the strength or magnitude of the noise.
- is the frequency, which determines how often the noise repeats.
- is time (or spatial position, if dealing with images).
- is the phase, indicating the starting point of the noise cycle.
Periodic noise often consists of multiple sinusoids at different frequencies, which form a harmonic series. This results in a more complex noise pattern that repeats at different intervals.
For example, consider periodic noise in a digital image, where it may appear as regular horizontal or vertical lines across the image. These lines correspond to a specific frequency at which the noise repeats. In an audio signal, periodic noise might present as a hum, such as the 50 or 60 Hz hum caused by electrical interference from power lines.
Periodic noise can cause significant problems because it interferes with the underlying signal or image in a predictable but disruptive way. In images, it can lead to distortions that obscure important details, while in audio, it can make it difficult to hear the original sound clearly.
To reduce or remove periodic noise, various techniques can be applied:
- Fourier Transform: This mathematical tool is used to identify the frequency components of the noise, allowing us to isolate and filter out the frequencies associated with the periodic noise.
- Notch Filters: These filters are designed to remove specific frequencies that correspond to the noise while preserving the rest of the signal.
- Band-Stop Filters: These filters remove a range of frequencies, effectively reducing the noise without affecting the entire signal.
Periodic noise can arise in a variety of situations, including:
- Electrical systems causing interference in both audio and image signals.
- Mechanical vibrations affecting cameras or other imaging systems, introducing unwanted patterns into images.
- Data communication systems where interference can lead to recurring errors or distortions in transmitted signals.
Estimation of Noise Parameters
Estimation of Noise Parameters is crucial in signal processing, communications, control systems, and various fields where the accurate modeling of noise helps to improve the performance of systems. Noise refers to unwanted disturbances or fluctuations that degrade the quality of the signal or measurement. To analyze and mitigate noise, it’s essential to estimate key noise parameters, including noise variance, mean, and sometimes the power spectral density (PSD).
Key Noise Parameters
- Noise Mean ()
This is the average or expected value of the noise process. For many noise types, such as Gaussian noise, the mean is zero, meaning there is no systematic bias introduced by the noise.
Mathematical Definition:
where is the noise sample at time , and is the total number of samples.
- Noise Variance ()
The variance represents the spread of the noise around the mean. It quantifies how much the noise deviates from its average value.
Mathematical Definition:
For white Gaussian noise, the variance is a critical parameter as it defines the noise power.
- Noise Power Spectral Density (PSD)
The PSD gives the distribution of noise power over different frequency components. It is especially useful in the analysis of continuous-time signals and systems.
Mathematical Definition:
where is the Fourier transform of the noise process over time duration , and is the power spectral density as a function of frequency .
Common Noise Models and Estimation Techniques
- Additive White Gaussian Noise (AWGN)
In AWGN, the noise is modeled as a normal distribution with zero mean and constant power across all frequencies.
- Mean Estimation Example:
Suppose you have a noisy signal , where is the true signal and is white Gaussian noise.
To estimate the noise mean:
where are the observed noisy signal samples.
- Variance Estimation Example:
To estimate the noise variance, subtract the mean from the noisy signal and compute:
- Colored Noise
Colored noise has a power spectral density that varies with frequency. Examples include pink noise, where the PSD decreases as frequency increases.
Estimating noise parameters in colored noise involves analyzing the autocorrelation or applying filtering techniques to isolate noise in specific frequency bands.
Estimation Methods
- Method of Moments
This method relies on calculating sample moments (e.g., sample mean and variance) from observed data. The first and second moments correspond to the mean and variance of the noise, respectively.
Example: For a noisy signal , where is the noise, the sample mean and sample variance can be computed as:
These estimates are used to approximate the actual noise parameters.
- Maximum Likelihood Estimation (MLE)
MLE is a widely used statistical method for estimating parameters of probabilistic models. For Gaussian noise, the MLE for the mean and variance are identical to the method of moments estimates.
Example: If the noise follows a Gaussian distribution, the MLE estimates for the mean () and variance () are:
Kalman Filter
The Kalman filter is an adaptive filter used in real-time noise estimation. It is effective in dynamic systems where noise parameters may vary over time. It operates by predicting the system state and updating the estimate based on new observations, minimizing the mean square error.Power Spectral Estimation
Estimating the PSD involves calculating the Fourier transform of the noise signal and averaging its squared magnitude. A practical method for PSD estimation is using the Welch method, which divides the signal into overlapping segments, computes the periodogram of each, and averages them.
Example: Noise Parameter Estimation in Communications
Suppose you are dealing with a communication system where a transmitted signal is corrupted by AWGN with unknown variance.
- Problem: Estimate the noise variance to understand how much noise is affecting the signal.
- Solution:
- Observe the received signal , where is the transmitted signal, and is the noise.
- Assume is known or can be estimated, so subtract the signal from the observation:
- Estimate the noise variance using: If , the variance can be simplified as:
References
- Gonzalez, R. C., & Woods, R. E. (2018). Digital Image Processing (4th ed.). Pearson.
- Jain, A. K. (1989). Fundamentals of Digital Image Processing. Prentice Hall.
- Buades, A., Coll, B., & Morel, J.-M. (2005). A Non-Local Algorithm for Image Denoising. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2, 60-65.
- Donoho, D. L., & Johnstone, I. M. (1994). Ideal Spatial Adaptation by Wavelet Shrinkage. Biometrika, 81(3), 425-455.
