In digital image and signal processing, noise is a common problem that can degrade the quality of data. Among various types of noise, periodic noise is particularly challenging due to its structured and repetitive nature. Unlike random noise, which occurs unpredictably, periodic noise manifests as repetitive interference patterns, often caused by mechanical vibrations, electronic interference, or other cyclic disturbances.
Frequency domain filtering offers a powerful method for dealing with this type of noise. By transforming the image or signal into the frequency domain using techniques like the Fourier Transform, periodic noise appears as concentrated bursts of energy at specific frequencies. This allows for precise identification and removal of the noise without significantly affecting the underlying data.
In this article, we will explore the concept of periodic noise, how it can be visualized in the frequency domain, and the various filtering techniques—such as bandreject, bandpass, and notch filters—that are used to reduce periodic noise effectively. These selective filters target specific frequency bands, providing a more focused and efficient approach to noise reduction compared to spatial domain methods.
Bandreject Filters
In the world of digital image and signal processing, noise reduction is a critical task for enhancing the quality and accuracy of data. One of the most effective techniques for removing noise in the frequency domain is the use of bandreject filters. These filters are specifically designed to attenuate or eliminate noise that occurs within a particular range of frequencies while preserving the rest of the signal or image.
Bandreject filters are particularly useful for combating periodic noise, a type of structured noise that appears as repetitive patterns in signals or images. By applying a bandreject filter, we can remove the noise while minimizing the loss of important information. This article will explore the mathematical concepts behind bandreject filters, their types, and practical examples to illustrate their application.
What is a Bandreject Filter?
A bandreject filter (also known as a bandstop filter) is a frequency domain filter that blocks or attenuates frequencies within a specific range, known as the stopband, while allowing frequencies outside this range to pass through unaffected.
Transfer Function of a Bandreject Filter
In mathematical terms, the behavior of a bandreject filter is described by its transfer function, , which defines how the filter modifies the frequency components of the image or signal. The transfer function for a bandreject filter can be defined as:
where:
- is the distance from the origin of the frequency plane to the point ,
- is the center frequency of the band to be rejected,
- is the width of the band of frequencies to be filtered.
This ideal bandreject filter sharply eliminates frequencies within the specified band, though such sharp transitions may cause unwanted artifacts like ringing due to the Gibbs phenomenon. To address this, Butterworth and Gaussian bandreject filters offer smoother alternatives.
Types of Bandreject Filters
There are three main types of bandreject filters: ideal, Butterworth, and Gaussian. Each type has a different approach to how it attenuates frequencies and transitions between the passband (frequencies allowed to pass) and the stopband (frequencies rejected).
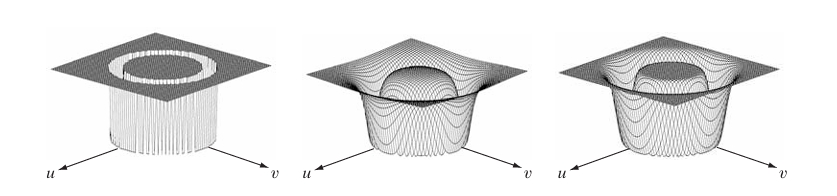
1. Ideal Bandreject Filter
The ideal bandreject filter has a perfectly sharp transition between the passband and the stopband. It completely removes all frequencies within the stopband but can introduce artifacts due to its abrupt nature.
The transfer function of an ideal bandreject filter is defined as:
This means that any frequency component within the range is fully suppressed.
Example:
Let’s assume we want to remove periodic noise with a center frequency and a band of frequencies with a width . The ideal bandreject filter will completely attenuate frequencies in the range while allowing all other frequencies to pass. However, due to the sharp transitions, this filter may introduce artifacts such as ringing.
2. Butterworth Bandreject Filter
The Butterworth bandreject filter offers a smoother transition between the passband and stopband, reducing the likelihood of introducing artifacts. It does not sharply cut off the frequencies within the stopband but gradually attenuates them.
The transfer function for an nth-order Butterworth bandreject filter is given by:
where:
- is the distance from the origin of the frequency plane to the point ,
- is the center frequency of the band to be rejected,
- is the width of the stopband,
- is the order of the filter, controlling the steepness of the transition.
Example:
Consider a Butterworth bandreject filter with , , and . This filter will gradually attenuate frequencies within the range and smoothly transition between the passband and stopband. As a result, it avoids introducing ringing artifacts but may leave behind some residual noise compared to the ideal filter.
3. Gaussian Bandreject Filter
The Gaussian bandreject filter provides the smoothest transition between the passband and stopband, making it the least likely to introduce artifacts. This filter is based on the Gaussian distribution and gradually reduces the magnitude of frequencies within the stopband.
The transfer function of the Gaussian bandreject filter is given by:
This equation ensures that frequencies near are attenuated smoothly without creating sharp edges in the frequency domain.
Example:
Using a Gaussian bandreject filter with and , the filter will reduce frequencies in the range in a gradual manner. This results in the least amount of artifacts while providing effective noise reduction.
Practical Example: Bandreject Filter Application
Consider a grayscale image that has been corrupted by periodic noise at a frequency of 60 Hz. The periodic noise shows up as a series of bright spots in the Fourier transform of the image. To remove this noise, we can apply a bandreject filter to target the specific frequency range around 60 Hz.
Step 1: Fourier Transform
First, we compute the Fourier Transform of the noisy image, which converts the image from the spatial domain to the frequency domain. The periodic noise will appear as distinct spikes at specific frequencies in the Fourier spectrum.
Step 2: Apply the Bandreject Filter
Next, we apply a bandreject filter that targets the frequencies around 60 Hz. Depending on the sharpness and smoothness we want, we can choose between an ideal, Butterworth, or Gaussian bandreject filter.
For this example, we use a Butterworth bandreject filter with Hz, a width , and an order . This filter will attenuate the noise while preserving most of the original image information.
Step 3: Inverse Fourier Transform
Finally, we apply the Inverse Fourier Transform to convert the filtered image back to the spatial domain. The result is a clean image with the periodic noise significantly reduced, while the essential image details remain intact.
filters
Bandpass Filters
In digital signal and image processing, noise reduction and signal enhancement are crucial for improving the quality of data. One of the most effective ways to isolate and extract specific frequency components is by using a bandpass filter. A bandpass filter allows frequencies within a certain range (the passband) to pass through while attenuating frequencies outside this range, including both low and high frequencies.
Bandpass filters are widely used in applications such as audio signal processing, telecommunications, and image processing, where it is essential to retain or emphasize specific frequencies while suppressing noise or unwanted signals.
What is a Bandpass Filter?
A bandpass filter is a frequency domain filter designed to allow frequencies within a certain range (passband) to pass through while rejecting or attenuating all frequencies outside that range. Bandpass filters are especially useful when we want to focus on a specific frequency band, such as in audio equalization or to extract periodic structures in an image.
The range of frequencies allowed by a bandpass filter is defined by two parameters:
- Lower cutoff frequency () – the lowest frequency that can pass through the filter.
- Upper cutoff frequency () – the highest frequency that can pass through the filter.
The bandwidth of the filter is the difference between the upper and lower cutoff frequencies:
Mathematical Concept of Bandpass Filters
The behavior of a bandpass filter is governed by its transfer function , which describes how the filter modifies frequency components. The general transfer function for a bandpass filter is derived from the combination of a low-pass filter and a high-pass filter. Mathematically, it can be expressed as:
Where:
- allows high frequencies to pass while attenuating low frequencies.
- allows low frequencies to pass while attenuating high frequencies.
By combining these two filters, the resulting bandpass filter allows frequencies within a specific range to pass while attenuating everything else.
Types of Bandpass Filters
Similar to other frequency domain filters, there are three main types of bandpass filters: ideal, Butterworth, and Gaussian. Each type has its own mathematical characteristics and practical applications.
1. Ideal Bandpass Filter
The ideal bandpass filter has a perfectly sharp transition between the passband and the stopband. It completely eliminates frequencies outside the passband, which can introduce ringing artifacts in the time or spatial domain due to the sharp transitions.
The transfer function of an ideal bandpass filter is:
where:
- is the lower cutoff frequency,
- is the upper cutoff frequency,
- is the distance from the origin of the frequency plane to the point .
This filter passes only the frequencies between and , rejecting all other frequencies. However, the abrupt cutoff can lead to unwanted artifacts in the output.
Example:
Suppose we want to isolate frequencies between 20 Hz and 100 Hz in a noisy signal. The ideal bandpass filter would allow only these frequencies to pass through, cutting off all frequencies below 20 Hz and above 100 Hz. However, the sharp cutoff may cause ringing in the time domain.
2. Butterworth Bandpass Filter
The Butterworth bandpass filter provides a smoother transition between the passband and the stopbands compared to the ideal filter. This helps reduce the introduction of artifacts such as ringing.
The transfer function for an nth-order Butterworth bandpass filter is:
Where:
- is the bandwidth (difference between and ),
- is the order of the filter (higher values of result in sharper transitions between passband and stopband).
Example:
Let’s apply a Butterworth bandpass filter to a signal where we want to keep frequencies between 20 Hz and 100 Hz, using a second-order filter. The Butterworth filter will smoothly attenuate frequencies outside this range, avoiding the harsh transitions that an ideal filter would introduce.
3. Gaussian Bandpass Filter
The Gaussian bandpass filter is the smoothest of the three and has the least risk of introducing artifacts into the signal or image. The transitions between the passband and stopband occur very gradually.
The transfer function for the Gaussian bandpass filter is given by:
where:
- is the center frequency of the bandpass filter,
- is the bandwidth (the difference between and ).
This filter is ideal for applications requiring very smooth filtering without introducing noticeable distortions.
Example:
Suppose we are working with a medical image containing periodic structures within a specific frequency range. A Gaussian bandpass filter with a center frequency and a bandwidth can be applied to emphasize those structures while minimizing noise and artifacts.
Practical Example: Bandpass Filter in Image Processing
Consider a grayscale image containing periodic patterns with frequencies ranging between 30 Hz and 70 Hz, along with noise from other frequency ranges. We can use a bandpass filter to isolate and emphasize these periodic patterns while removing the noise.
Step 1: Fourier Transform
First, we compute the Fourier Transform of the image to convert it from the spatial domain to the frequency domain. The periodic patterns will appear as spikes in the frequency spectrum at certain points.
Step 2: Apply the Bandpass Filter
We apply a Butterworth bandpass filter with lower and upper cutoff frequencies of 30 Hz and 70 Hz. This filter will allow frequencies in this range to pass while attenuating all other frequencies, reducing noise and enhancing the periodic patterns.
Step 3: Inverse Fourier Transform
Finally, we apply the Inverse Fourier Transform to convert the filtered image back to the spatial domain. The resulting image will emphasize the desired periodic structures and remove unwanted noise outside the specified frequency band.

Notch Filters
In digital signal and image processing, noise and interference can severely degrade the quality of data. A particularly effective technique for removing specific, unwanted frequencies is the notch filter. Unlike bandreject filters, which block a range of frequencies, a notch filter is designed to remove a very narrow band of frequencies while leaving the rest of the signal or image unaffected. This makes notch filters ideal for eliminating periodic noise or interference that occurs at specific frequencies.
Notch filters are widely used in applications like audio signal processing, communications, and image restoration, where it’s crucial to remove a single frequency or a few unwanted frequencies without affecting the entire frequency spectrum.
What is a Notch Filter?
A notch filter is a frequency domain filter that blocks or attenuates a very narrow band of frequencies centered around a specific frequency (the notch), while allowing all other frequencies to pass. This makes them particularly useful for removing noise or interference caused by a specific frequency, such as power line interference at 60 Hz in electrical systems.
Notch filters are closely related to bandreject filters, but their defining characteristic is the narrow bandwidth around the notch frequency, making them highly selective in their filtering behavior.
Mathematical Concept of Notch Filters
The behavior of a notch filter is described by its transfer function, , which indicates how the filter affects different frequency components. A notch filter attenuates frequencies in a narrow band around the notch frequency, , while allowing all other frequencies to pass. Mathematically, the transfer function can be defined as:
where:
- is the distance from the origin in the frequency domain to the point ,
- is the specific frequency where the notch filter will block or attenuate.
The notch filter essentially “notches out” the frequency at and allows all other frequencies to remain intact.
Types of Notch Filters
There are several variations of notch filters, including ideal, Butterworth, and Gaussian notch filters. Each type has different characteristics and practical applications, especially when it comes to how sharply the filter attenuates the unwanted frequency and how smoothly it transitions between the notch and passband.
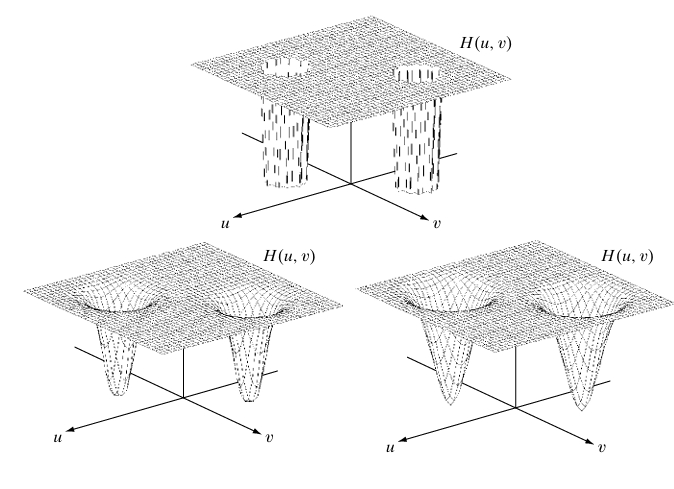
1. Ideal Notch Filter
The ideal notch filter completely removes a specific frequency and has an extremely sharp transition between the attenuated and unattenuated frequencies. It is mathematically expressed as:
This filter is highly effective at removing periodic noise caused by a single frequency but can introduce artifacts in the filtered signal or image due to the sharp cutoff.
Example:
If we need to remove interference caused by a 60 Hz power line in an audio signal, an ideal notch filter would completely eliminate all frequency components at exactly 60 Hz, while leaving all other frequencies unaffected. However, this sharp cutoff may result in distortion or ringing artifacts.
2. Butterworth Notch Filter
The Butterworth notch filter offers a smoother transition between the notch and the passband, reducing the risk of artifacts like ringing. The transfer function for a Butterworth notch filter of order is given by:
where:
- is the center frequency of the notch,
- is the distance from the origin of the frequency domain to the point ,
- is the order of the filter, controlling the sharpness of the transition between the notch and the passband.
This filter is more practical than the ideal notch filter because it reduces unwanted artifacts while still effectively attenuating the specific frequency.
Example:
Using a second-order Butterworth notch filter to remove a 60 Hz interference, the filter will attenuate the 60 Hz frequency smoothly, without introducing sharp transitions. This is particularly useful in audio applications where we want to remove specific interference while preserving the quality of the signal.
3. Gaussian Notch Filter
The Gaussian notch filter provides the smoothest transition between the notch and passband, making it the least likely to introduce artifacts. It is based on the Gaussian distribution, which ensures that the attenuation of frequencies is gradual and seamless.
The transfer function for a Gaussian notch filter is given by:
where:
- is the center frequency of the notch,
- controls the width of the notch (the range of frequencies around that will be attenuated),
- is the distance from the origin of the frequency plane.
Example:
A Gaussian notch filter with Hz and a small can be applied to remove power line interference smoothly from an audio or image signal, ensuring that no harsh artifacts are introduced. This type of filter is commonly used in applications where maintaining the overall quality of the signal is critical.
Practical Example: Removing Periodic Noise with a Notch Filter
Let’s consider an image that has been corrupted by periodic noise at a specific frequency due to interference. The noise appears as periodic vertical stripes in the spatial domain, which corresponds to a specific frequency in the Fourier transform.
Step 1: Fourier Transform
First, we compute the Fourier Transform of the noisy image to convert it from the spatial domain to the frequency domain. The periodic noise will appear as distinct peaks (spikes) in the frequency spectrum at specific points corresponding to the noise frequency.
Step 2: Apply the Notch Filter
Next, we apply a Butterworth notch filter centered at the frequency of the noise peaks. This filter will attenuate the frequencies causing the periodic noise without affecting the rest of the image.
Step 3: Inverse Fourier Transform
After applying the notch filter, we compute the Inverse Fourier Transform to convert the image back to the spatial domain. The result is a clean image with the periodic noise effectively removed, while the original image information is preserved.
Applications of Notch Filters
- Audio Signal Processing: Notch filters are commonly used to remove unwanted frequencies from audio signals, such as eliminating the hum caused by electrical interference at 50/60 Hz.
- Image Processing: In image restoration, notch filters can remove periodic noise patterns, such as scanline interference in old images or digital artifacts from camera sensors.
- Telecommunications: In communication systems, notch filters are employed to block out specific interference frequencies while ensuring that the transmitted signal remains clear.
- Medical Imaging: Notch filters can be used to eliminate specific frequency artifacts in medical imaging modalities like MRI or CT scans, enhancing the quality of diagnostic images.
Optimum Notch Filtering
Optimum Notch Filtering is a technique used in signal processing and image processing to remove or reduce specific unwanted frequency components (like noise) from a signal. This is particularly useful when the noise affects only certain frequencies, which makes it different from other filters that remove a broad range of frequencies.
Notch Filter Concept
A notch filter is designed to remove a narrow band of frequencies from a signal, keeping the other frequencies intact. It’s like a specialized version of a band-stop filter, but much narrower. The “optimum” part of optimum notch filtering refers to adjusting the filter parameters in the best possible way for the specific noise problem to ensure minimal loss of important signal content.
Mathematical Concepts
1. Frequency Domain Representation
Any signal can be transformed into its frequency components using the Fourier transform. The idea of notch filtering starts from analyzing the signal in the frequency domain because noise might be easier to identify and remove in this domain. For a signal , the Fourier transform gives us:
where:
- represents the frequency components of the signal,
- is the frequency,
- is the imaginary unit.
2. Ideal Notch Filter
An ideal notch filter can be represented by a transfer function in the frequency domain. It will pass all frequencies except those in a narrow band around the frequency to be eliminated.
This means that at the target frequency and its surrounding narrow band (from to ), the filter sets the signal to 0 (i.e., removing it).
3. Practical Notch Filter
In practice, filters aren’t perfect, so we use a smoother second-order transfer function for a more realistic notch filter:
where:
- is the notch frequency (the frequency to be removed),
- is the damping factor that controls the width of the notch,
- is the bandwidth of the notch.
The bandwidth can be adjusted so that only a narrow range of frequencies around is removed.
4. Inverse Filtering
In some cases, if the noise has been removed too aggressively, some of the signal may be lost. Inverse filtering can be used to restore the original signal, which balances signal preservation with noise removal.
This inverse filter is applied to restore frequencies outside the removed notch band.
Example of Optimum Notch Filtering
Suppose we have a signal containing noise at a specific frequency, say 60 Hz (common in electrical systems). We want to filter out this noise while preserving the rest of the signal.
Step 1: Fourier Transform First, take the Fourier transform of the signal to identify the 60 Hz noise.
Step 2: Design Notch Filter We design a notch filter with and a small bandwidth around this frequency, say , to create a narrow notch from 55 Hz to 65 Hz.
Step 3: Apply the Filter Apply the filter to the frequency domain representation of the signal. This will remove frequencies between 55 Hz and 65 Hz.
Step 4: Inverse Fourier Transform Convert the filtered signal back to the time domain using the inverse Fourier transform, which gives us the cleaned signal without the 60 Hz noise.
- Optimization To optimize, we adjust the parameters of the filter (e.g., or bandwidth ) to balance noise reduction and signal preservation. The goal is to eliminate the unwanted frequency without distorting the rest of the signal.
Applications
Optimum notch filtering is widely used in:
- Audio Processing: Removing powerline hum (usually at 50 Hz or 60 Hz).
- Medical Imaging: Reducing periodic noise in MRI or ECG signals.
- Image Processing: Filtering periodic interference patterns in images.
By carefully designing the notch filter, unwanted noise can be removed while keeping the important part of the signal intact.
Difference between Optimum Notch Filtering and Notch Filtering
The key difference between Optimum Notch Filtering and Notch Filtering lies in the level of precision and customization used when designing the filter. Let’s break down the two terms:
1. Notch Filtering
A Notch Filter is a general filter that removes or reduces a narrow band of frequencies from a signal, leaving other frequencies mostly unaffected. The filter can be applied in both analog and digital domains and is typically used when the noise or interference in a signal is concentrated around a specific frequency or small range of frequencies. It is called a “notch” filter because it creates a notch (or dip) in the frequency spectrum at the targeted frequency.
- Purpose: To eliminate a narrow band of unwanted frequencies, like removing 50 Hz or 60 Hz hum from an electrical signal.
- Design: Simple design, often with fixed parameters such as center frequency and bandwidth.
- Flexibility: Limited flexibility; once designed, the filter is typically applied uniformly without further tuning.
Example:
In audio processing, if there’s a hum at 60 Hz due to powerline interference, a standard notch filter can be designed with a center frequency of 60 Hz to eliminate that hum.
2. Optimum Notch Filtering
Optimum Notch Filtering is a more sophisticated approach where the filter parameters (such as bandwidth, damping factor, and frequency range) are carefully optimized to achieve the best balance between removing the noise and preserving the original signal. The goal is to fine-tune the filter to the specific characteristics of the noise and the signal, ensuring that the filtering does not remove more than necessary.
- Purpose: To precisely remove noise at a specific frequency while minimizing the loss of important signal content.
- Design: Parameters like the center frequency, bandwidth, and damping are optimized based on the noise characteristics and signal needs.
- Flexibility: Highly flexible; the filter can be adjusted dynamically for different types of noise and signals to maximize performance.
Key Elements of Optimization:
- Adaptive Filtering: In some cases, the filter can adapt over time as the noise or signal characteristics change.
- Damping Factor (): Controls the sharpness of the notch. A higher damping factor can widen the notch, but may affect neighboring frequencies more.
- Bandwidth (): Adjusted carefully to ensure only the unwanted noise frequencies are removed, keeping the rest of the signal intact.
Example:
In medical imaging, where precise information from a signal like an ECG or MRI must be preserved, an optimum notch filter would carefully remove periodic noise (e.g., from an electrical source) without distorting the medical data. The parameters would be adjusted for that specific noise profile to ensure the cleanest possible signal.
Key Differences
| Feature | Notch Filtering | Optimum Notch Filtering |
|---|---|---|
| Purpose | General removal of narrow frequency bands | Fine-tuned removal of specific noise with minimal signal loss |
| Flexibility | Limited; standard, non-adaptive | Highly flexible; parameters optimized for specific situations |
| Parameter Tuning | Fixed parameters | Dynamically adjustable to achieve optimal results |
| Complexity | Relatively simple | More complex, involving analysis and tuning |
| Application | Basic noise removal tasks | Critical applications needing signal preservation, e.g., medical imaging, precision audio |
References
- Gonzalez, R. C., & Woods, R. E. (2018). Digital Image Processing. Pearson.
- Oppenheim, A. V., Willsky, A. S., & Nawab, S. H. (1997). Signals and Systems. Prentice Hall.
- Proakis, J. G., & Manolakis, D. G. (2007). Digital Signal Processing: Principles, Algorithms, and Applications. Pearson.
- Sörgel, W., & Wiesbeck, W. (2012). Signal Processing for Communications. John Wiley & Sons.
