Prefix Codes

Definition and Properties

Prefix Codes

A prefix code is a set of codewords such that no codeword is a prefix of another. Formally, for a set of codewords $C = \{c_1, c_2, \ldots, c_n\}$ over an alphabet $A$, the prefix condition states:

where $c_i \not\prec c_j$ means $c_i$ is not a prefix of $c_j$.

Example:

The code $C = \{0, 10, 110\}$ is a prefix code because no codeword is a prefix of another. In contrast, $C = \{0, 01, 10\}$ is not a prefix code because “0” is a prefix of “01”.

Properties of Prefix Codes

1. Instantaneous Decoding: Since no codeword is a prefix of another, a prefix code can be decoded as soon as a codeword is encountered in the input stream.
2. Uniquely Decodable: All prefix codes are uniquely decodable, but not all uniquely decodable codes are prefix codes.
3. Kraft-McMillan Inequality: Prefix codes satisfy the Kraft-McMillan inequality: $$\sum_{i=1}^n D^{-l_i} \leq 1$$ where $l_i$ is the length of the $i$-th codeword and $D$ is the size of the alphabet.

Mathematical Foundation

Kraft-McMillan Inequality

Theorem:

For any prefix code over a $D$-ary alphabet, the lengths of the codewords $\{l_1, l_2, \ldots, l_n\}$ must satisfy:

Proof (Sketch):

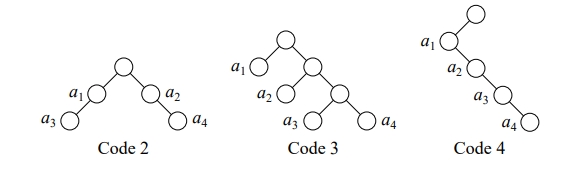
1. Assign a binary tree structure to the codewords, where each node represents a decision.
2. Each codeword corresponds to a unique path in the tree, and the lengths $l_i$ determine the depths of the nodes.
3. The sum $D^{-l_i}$ represents the fraction of the tree’s capacity used by each codeword.
4. Since the tree cannot exceed its full capacity, the inequality holds.

If equality is achieved ($\sum_{i=1}^n D^{-l_i} = 1$), the code is maximally efficient.

Construction of Prefix Codes

Huffman Coding

Huffman coding is a popular method for constructing optimal prefix codes. It minimizes the average codeword length for a given set of symbol probabilities.

Algorithm:

1. Begin with a list of symbols and their probabilities.
2. Combine the two least probable symbols into a new node.
3. Assign binary labels (e.g., 0 and 1) to the branches of the combined node.
4. Repeat until a single tree remains.

Python Implementation

Example: Check Prefix Code

The following Python code checks if a given set of codewords forms a prefix code.

python
def is_prefix_code(codewords):
    """
    Determines if a set of codewords is a prefix code.
    """
    for i, word1 in enumerate(codewords):
        for j, word2 in enumerate(codewords):
            if i != j and word2.startswith(word1):
                return False  # word1 is a prefix of word2
    return True

# Example
codewords = ["0", "10", "110"]
print("Is Prefix Code:", is_prefix_code(codewords))  # Output: True

Example: Huffman Coding

The following Python code constructs a Huffman tree and generates prefix codes.

python
import heapq
from collections import defaultdict

def huffman_coding(symbols, probabilities):
    """
    Constructs a Huffman tree and generates prefix codes.
    """
    heap = [[prob, [symbol, ""]] for symbol, prob in zip(symbols, probabilities)]
    heapq.heapify(heap)

    while len(heap) > 1:
        low1 = heapq.heappop(heap)
        low2 = heapq.heappop(heap)
        for pair in low1[1:]:
            pair[1] = '0' + pair[1]
        for pair in low2[1:]:
            pair[1] = '1' + pair[1]
        heapq.heappush(heap, [low1[0] + low2[0]] + low1[1:] + low2[1:])

    return sorted(heapq.heappop(heap)[1:], key=lambda p: (len(p[-1]), p))

# Example
symbols = ['A', 'B', 'C', 'D']
probabilities = [0.4, 0.3, 0.2, 0.1]
huffman_codes = huffman_coding(symbols, probabilities)
print("Huffman Codes:", huffman_codes)

Applications of Prefix Codes

1. Data Compression: Prefix codes are used in lossless compression algorithms like Huffman coding and Shannon-Fano coding.
2. Networking: Efficient packet encoding in data transmission.
3. Cryptography: Ensuring unique decoding in secure communications.