Preliminary Concepts in Image Processing

Complex Numbers are a fundamental concept in mathematics and have numerous applications in image processing, particularly in operations involving transformations, filtering, and frequency analysis. They provide a way to represent both magnitude and phase information, which is crucial for tasks such as Fourier Transform, image rotation, and filtering in the frequency domain.

Definition of Complex Numbers

A complex number is a number of the form:

where:

• $a$ is the real part of the complex number.
• $b$ is the imaginary part of the complex number.
• $i$ is the imaginary unit, defined by the property $i^2 = -1$.

Representation of Complex Numbers

1. Rectangular Form (Cartesian Form):

   A complex number $z$ can be represented as:

   $$z = a + bi$$

   where $a$ and $b$ are real numbers.

2. Polar Form:

   A complex number can also be represented in polar form using its magnitude (or modulus) $r$ and angle (or argument) $\theta$:

   $$z = r (\cos \theta + i \sin \theta)$$
   • $r = |z| = \sqrt{a^2 + b^2}$ is the magnitude of the complex number.
   • $\theta = \arg(z) = \tan^{-1} \left( \frac{b}{a} \right)$ is the argument (angle) of the complex number in radians.

   The polar form can also be written using Euler’s formula:

   $$z = r e^{i \theta}$$

   where $e^{i \theta} = \cos \theta + i \sin \theta$.

Basic Operations with Complex Numbers

1. Addition and Subtraction:

   If $z_1 = a_1 + b_1i$ and $z_2 = a_2 + b_2i$, then:

   $$z_1 + z_2 = (a_1 + a_2) + (b_1 + b_2)i$$ $$z_1 – z_2 = (a_1 – a_2) + (b_1 – b_2)i$$

2. Multiplication:

   If $z_1 = a_1 + b_1i$ and $z_2 = a_2 + b_2i$, then:

   $$z_1 \cdot z_2 = (a_1 a_2 – b_1 b_2) + (a_1 b_2 + a_2 b_1)i$$

3. Division:

   To divide two complex numbers $z_1 = a_1 + b_1i$ and $z_2 = a_2 + b_2i$:

   $$\frac{z_1}{z_2} = \frac{a_1 + b_1i}{a_2 + b_2i} = \frac{(a_1 + b_1i)(a_2 – b_2i)}{a_2^2 + b_2^2}$$

4. Conjugate of a Complex Number:

   The conjugate of a complex number $z = a + bi$ is:

   $$\overline{z} = a – bi$$

   The product of a complex number and its conjugate gives its magnitude squared:

   $$z \cdot \overline{z} = (a + bi)(a – bi) = a^2 + b^2 = |z|^2$$

Applications of Complex Numbers in Image Processing

1. Fourier Transform:

   The Fourier Transform is a mathematical tool used to transform an image from the spatial domain to the frequency domain. In the frequency domain, an image is represented using complex numbers. The transform is given by:

   $$F(u, v) = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) \cdot e^{-i 2 \pi \left( \frac{ux}{M} + \frac{vy}{N} \right)}$$

   where:

   • $f(x, y)$ is the image in the spatial domain.
   • $F(u, v)$ is the image in the frequency domain.
   • $M$ and $N$ are the dimensions of the image.

   The complex numbers in the Fourier Transform contain both the magnitude (indicating how strong a frequency is) and the phase (indicating the position of that frequency in the image).

2. Image Rotation:

   Complex numbers can represent points in 2D space, and multiplication by a complex number in polar form can be used to rotate an image. To rotate a point $(x, y)$ by an angle $\theta$:

   $$z = x + yi \quad \text{(convert to complex number)}$$

   Rotate by multiplying by $e^{i \theta}$:

   $$z’ = z \cdot e^{i \theta} = (x + yi)(\cos \theta + i \sin \theta)$$

   The new coordinates after rotation are:

   $$x’ = x \cos \theta – y \sin \theta, \quad y’ = x \sin \theta + y \cos \theta$$

3. Filtering in Frequency Domain:

   In image processing, filtering is often more efficient in the frequency domain. After applying the Fourier Transform to convert the image to the frequency domain, complex numbers are used to represent and manipulate the image. For example, a low-pass filter can be applied to remove high-frequency noise by multiplying the frequency representation of the image by a filter function $H(u, v)$.

   If $F(u, v)$ is the Fourier Transform of the image and $H(u, v)$ is the filter:

   $$G(u, v) = F(u, v) \cdot H(u, v)$$

   The result is then transformed back to the spatial domain using the Inverse Fourier Transform:

   $$g(x, y) = \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} G(u, v) \cdot e^{i 2 \pi \left( \frac{ux}{M} + \frac{vy}{N} \right)}$$

Example: Complex Numbers in Image Processing

Example 1: Image Rotation using Complex Numbers

Suppose we have a point in the image at coordinates $(3, 4)$ and we want to rotate it by 45 degrees ($\theta = 45^\circ$).

1. Convert the point to a complex number:

   $$z = 3 + 4i$$

2. Convert the rotation angle to radians:

   $$\theta = 45^\circ = \frac{\pi}{4} \text{ radians}$$

3. Multiply by the complex exponential $e^{i \theta}$:

   $$e^{i \frac{\pi}{4}} = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} = \frac{\sqrt{2}}{2} + i \frac{\sqrt{2}}{2}$$ $$z’ = (3 + 4i) \cdot \left( \frac{\sqrt{2}}{2} + i \frac{\sqrt{2}}{2} \right)$$

4. Perform the multiplication:

   $$z’ = (3 \cdot \frac{\sqrt{2}}{2} – 4 \cdot \frac{\sqrt{2}}{2}) + i (3 \cdot \frac{\sqrt{2}}{2} + 4 \cdot \frac{\sqrt{2}}{2})$$ $$z’ = (-\sqrt{2}/2) + i (7\sqrt{2}/2)$$

   Thus, the rotated coordinates are approximately $(-0.707, 4.95)$.

Complex numbers play a critical role in image processing, enabling powerful mathematical operations for tasks such as frequency analysis, rotation, and filtering. Understanding how to work with complex numbers, including their various forms and operations, is essential for anyone involved in the field of image processing.

The Fourier Transform is a mathematical tool that transforms a function from its original domain (often time or space) into the frequency domain. It is widely used in fields such as signal processing, physics, and engineering to analyze the frequencies present in a signal.

Concepts Behind the Fourier Transform

1. Continuous Functions and Periodicity:
   The Fourier Transform is typically applied to continuous functions, $f(x)$, where $x$ is a continuous variable representing time (in the case of a time-domain signal) or space (in the case of a spatial-domain signal).

2. Decomposition into Sinusoids:
   The core idea is that any continuous function can be decomposed into a sum (or integral) of sine and cosine functions (sinusoids) of varying frequencies. This decomposition allows us to analyze the “frequency content” of the original function.

3. Frequency Domain Representation:
   By transforming a function into the frequency domain, we shift from a representation of the function in terms of time or space to one in terms of frequencies. This is useful for understanding how different frequency components contribute to the overall function.

The Definition of the Fourier Transform

The Fourier Transform of a continuous function $f(x)$ is defined as:

where:

• $F(k)$ is the Fourier Transform of $f(x)$, a function of the frequency variable $k$.
• $f(x)$ is the original function.
• $e^{-2 \pi i k x}$ represents a complex exponential, which is a combination of sine and cosine functions due to Euler’s formula: $$e^{ix} = \cos(x) + i \sin(x).$$

Inverse Fourier Transform

The original function $f(x)$ can be recovered from its Fourier Transform $F(k)$ using the Inverse Fourier Transform:

This shows that the Fourier Transform is reversible, and no information is lost in the transformation process.

Key Properties of the Fourier Transform

1. Linearity:
   The Fourier Transform is a linear operation. If $f(x)$ and $g(x)$ are two functions, and $a$ and $b$ are constants, then:

   $$\mathcal{F}\{a f(x) + b g(x)\} = a \mathcal{F}\{f(x)\} + b \mathcal{F}\{g(x)\}.$$

2. Time/Frequency Shifting:

   • Time Shift: If $g(x) = f(x – x_0)$, then $\mathcal{F}\{g(x)\} = e^{-2 \pi i k x_0} F(k)$.
   • Frequency Shift: If $g(x) = e^{2 \pi i k_0 x} f(x)$, then $\mathcal{F}\{g(x)\} = F(k – k_0)$.

3. Scaling:
   If $g(x) = f(ax)$, where $a$ is a scaling factor, then:

   $$\mathcal{F}\{g(x)\} = \frac{1}{|a|} F\left(\frac{k}{a}\right).$$

4. Convolution Theorem:
   The Fourier Transform of the convolution of two functions is the product of their individual Fourier Transforms:

   $$\mathcal{F}\{f(x) * g(x)\} = F(k) G(k),$$

   where $(f * g)(x) = \int_{-\infty}^{\infty} f(t) g(x – t) \, dt$ is the convolution of $f$ and $g$.

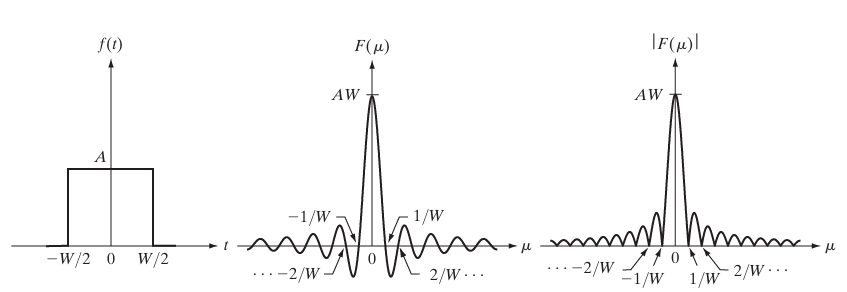
Example: Fourier Transform of a Gaussian Function

Let’s compute the Fourier Transform of a Gaussian function, which is a commonly used function in probability and statistics:

To find the Fourier Transform, we apply the definition:

Combine the exponentials:

Complete the square in the exponent:

Substitute back:

Since the integral of a Gaussian over all space is a constant (independent of the linear term), we have:

Applications of Fourier Transform

1. Signal Processing: Used to analyze and filter signals, detect frequencies, and compress data.
2. Image Processing: Used for image filtering, edge detection, and pattern recognition.
3. Quantum Mechanics: Describes the wave function in terms of momentum and position.
4. Data Analysis: Used to identify patterns, trends, and periodicities in datasets.

The Fourier Transform is a powerful mathematical tool for analyzing and understanding the frequency characteristics of functions. By converting functions from their original domain to the frequency domain, it provides deep insights into their behavior and is indispensable in many scientific and engineering fields.

Convolution in Image Processing is a fundamental operation used to modify or analyze images. It is widely employed in various image processing tasks, including blurring, sharpening, edge detection, and feature extraction. Convolution involves applying a filter (also called a kernel) to an image, transforming it into a new image that emphasizes specific features or patterns.

Mathematical Concepts Behind Convolution

1. Discrete Convolution Definition:
   Convolution is a mathematical operation that combines two functions to produce a third function. In the context of image processing, one function represents the image, and the other represents the filter or kernel. The discrete convolution of a 2D image $I(x, y)$ with a filter $K(x, y)$ is defined as:

   $$(I * K)(x, y) = \sum_{m=-M}^{M} \sum_{n=-N}^{N} I(x – m, y – n) \cdot K(m, n),$$

   where:

   • $I(x, y)$ is the original image.
   • $K(x, y)$ is the convolution kernel (filter), typically a small matrix like $3 \times 3$ or $5 \times 5$.
   • $(x, y)$ denotes the coordinates in the image.
   • $M$ and $N$ are the half-widths and half-heights of the kernel, respectively.

2. Kernel (Filter):
   The kernel is a matrix of weights that defines how each pixel in the input image influences the output pixel. The kernel can emphasize or suppress certain features, like edges, lines, or textures, depending on its values. Common kernels include those for blurring, sharpening, and edge detection.

3. Sliding Window Operation:
   Convolution in image processing is performed by sliding the kernel over the image. At each position of the kernel, a weighted sum of the pixel values covered by the kernel is calculated. This sum becomes the value of the corresponding pixel in the output image.

Steps in Convolution for Image Processing

1. Choose a Kernel:
   Select a kernel that represents the operation you want to perform (e.g., blur, sharpen, edge detect).

2. Slide the Kernel Over the Image:
   Place the kernel on top of the image at the starting pixel (usually at the top-left corner). Slide it across the image, one pixel at a time.

3. Calculate the Convolution:
   For each position of the kernel:

   • Multiply each value in the kernel by the corresponding pixel value in the image.
   • Sum all the multiplied values.
   • Replace the center pixel of the region under the kernel with this sum.

4. Repeat for All Pixels:
   Continue sliding the kernel across the entire image, repeating the calculation for each pixel.

Example: Convolution for Edge Detection

Let’s consider a simple example of convolution to detect edges in an image using the Sobel Operator. The Sobel operator is a commonly used edge detection kernel in image processing.

Sobel Kernels for Edge Detection

There are two Sobel kernels, one for detecting horizontal edges and another for detecting vertical edges:

• Horizontal Sobel Kernel (detects vertical edges):

• Vertical Sobel Kernel (detects horizontal edges):

Applying the Sobel Kernels

1. Input Image:
   Consider a small grayscale image represented by a matrix:

   $$I = \begin{bmatrix} 3 & 0 & 1 & 2 & 7 & 4 \\ 1 & 5 & 8 & 9 & 3 & 1 \\ 2 & 7 & 2 & 5 & 1 & 3 \\ 0 & 1 & 3 & 1 & 7 & 8 \\ 4 & 2 & 1 & 6 & 2 & 8 \\ 2 & 4 & 5 & 2 & 3 & 9 \end{bmatrix}$$

2. Applying the Horizontal Sobel Kernel $K_x$:

   To apply the convolution, we center the Sobel kernel over each pixel (except the border pixels, where padding may be needed) and compute the weighted sum. For simplicity, consider applying the kernel to the pixel at position (2, 2).

   The region of interest (ROI) of the image under the kernel is:

   $$\text{ROI} = \begin{bmatrix} 3 & 0 & 1 \\ 1 & 5 & 8 \\ 2 & 7 & 2 \end{bmatrix}$$

   Now, compute the convolution by multiplying each kernel value with the corresponding image pixel value and summing:

   $$(I * K_x)(2, 2) = (-1) \cdot 3 + 0 \cdot 0 + 1 \cdot 1 + (-2) \cdot 1 + 0 \cdot 5 + 2 \cdot 8 + (-1) \cdot 2 + 0 \cdot 7 + 1 \cdot 2$$

   Simplify the sum:

   $$= (-3) + 0 + 1 + (-2) + 0 + 16 + (-2) + 0 + 2 = 12.$$

   Thus, the output pixel value at position (2, 2) after applying the horizontal Sobel kernel is 12.

3. Repeat for All Pixels:
   Repeat the process for each pixel in the image, skipping the borders or using padding (zero-padding or replicate-padding) to handle border pixels.

4. Combining Results for Edge Magnitude:
   After applying both the horizontal $K_x$ and vertical $K_y$ Sobel kernels to the entire image, compute the edge magnitude at each pixel using:

   $$G(x, y) = \sqrt{(I * K_x)(x, y)^2 + (I * K_y)(x, y)^2}.$$

   This formula gives the strength of the edge at each pixel.

Properties of Convolution in Image Processing

1. Linearity:
   Convolution is a linear operation, meaning that the convolution of a sum of two images equals the sum of the convolutions of each image:

   $$(I_1 + I_2) * K = (I_1 * K) + (I_2 * K).$$

2. Commutativity:
   The convolution operation is commutative, meaning that:

   $$I * K = K * I.$$

3. Associativity:
   Convolution is associative, so:

   $$I * (K_1 * K_2) = (I * K_1) * K_2.$$

4. Distributivity:
   Convolution is distributive over addition:

   $$I * (K_1 + K_2) = (I * K_1) + (I * K_2).$$

Applications of Convolution in Image Processing

1. Blurring and Smoothing:
   Convolution with a kernel filled with equal weights (such as a Gaussian kernel) can blur an image by averaging neighboring pixels. This reduces noise and smooths the image.

2. Sharpening:
   Convolution with a sharpening kernel (e.g., Laplacian kernel) enhances the edges, making details more pronounced.

3. Edge Detection:
   Convolution with specific kernels like the Sobel or Prewitt operators highlights edges by detecting intensity changes.

4. Feature Extraction:
   Convolution is used in computer vision and deep learning for detecting patterns, textures, and features in images.

Convolution is a fundamental operation in image processing, providing the means to manipulate and analyze images by filtering and extracting useful information. It is the backbone of many algorithms, such as those for blurring, sharpening, edge detection, and even deep learning models for image recognition. Understanding convolution and its applications allows for effective image analysis and manipulation.