The 2-D Discrete Fourier Transform (DFT) is a powerful mathematical tool used to analyze the frequency content of two-dimensional signals, such as images. Just as the 1-D DFT is used to decompose signals into their constituent frequencies, the 2-D DFT extends this concept to functions of two variables, enabling the analysis of spatial frequencies in two dimensions. This is particularly useful in fields like image processing, pattern recognition, and computer vision, where understanding the frequency components of an image is crucial for tasks such as filtering, compression, and feature extraction.
Relationships Between Spatial and Frequency Intervals
In signal processing and image analysis, understanding the relationship between spatial and frequency intervals is crucial. This connection allows us to analyze how changes in the spatial domain of a signal or image influence its frequency representation and vice versa. This relationship is governed by the Fourier Transform, which transforms a signal from the spatial (or time) domain to the frequency domain.
Spatial and Frequency Domains
Spatial Domain:
In the spatial domain, a signal or an image is represented by its amplitude values at different points. For example, a 1D signal could be represented as , where is the spatial coordinate, and is the amplitude at . In a 2D image, it is represented as , where are the spatial coordinates and is the pixel value at that position.Frequency Domain:
The frequency domain represents how often the signal’s values change with respect to space (or time). The Fourier Transform maps the spatial representation into the frequency representation, resulting in for a 1D signal or for a 2D image, where and are the frequency components corresponding to the spatial coordinates and .
Fourier Transform and Its Properties
The Fourier Transform provides a relationship between the spatial and frequency domains. For a 1D continuous function , the Fourier Transform is given by:
The inverse Fourier Transform is:
For a 2D function , the 2D Fourier Transform is:
And its inverse is:
These transforms show how a function in the spatial domain can be expressed as a combination of sinusoids in the frequency domain.
Sampling and the Nyquist Theorem
When dealing with discrete signals or images, the sampling process plays a significant role in determining the relationship between spatial and frequency intervals. According to the Nyquist theorem, for a signal to be perfectly reconstructed from its samples, the sampling rate must be at least twice the maximum frequency present in the signal.
Sampling in 1D:
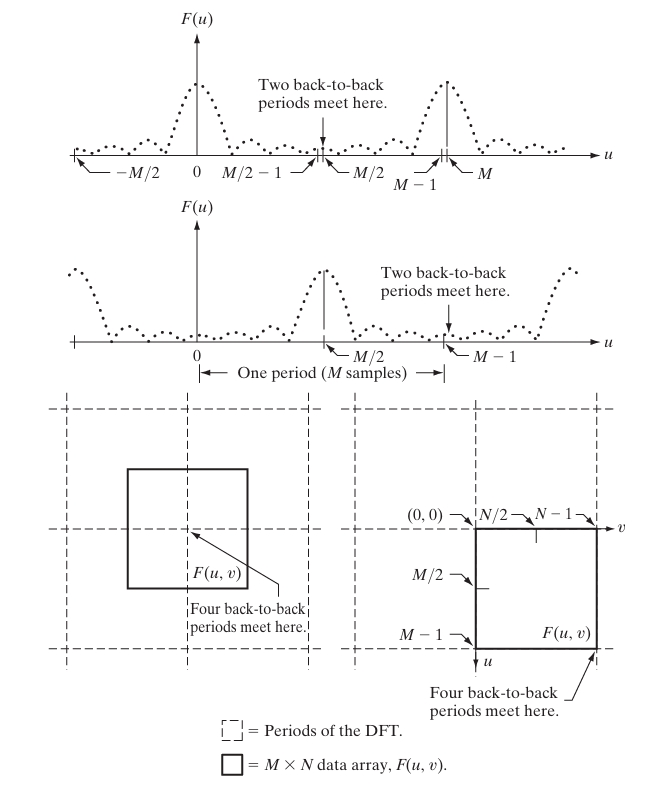
Consider a continuous signal sampled at intervals of . The sampling frequency is . The frequency interval in the discrete Fourier Transform is given by , where is the number of samples.Sampling in 2D:
For a 2D image sampled at intervals and along the – and -axes respectively, the sampling frequencies are and . The corresponding frequency intervals in the discrete Fourier Transform are and , where and are the number of samples along the – and -axes respectively.
Relationship Between Spatial and Frequency Intervals
The relationship between spatial and frequency intervals is inversely proportional. This means that as the spatial interval (or sampling interval) increases, the corresponding frequency interval decreases, and vice versa. This is due to the property of the Fourier Transform, which states that a narrow function in the spatial domain corresponds to a wide function in the frequency domain and vice versa.
Example:
Consider a 1D signal sampled at an interval .
Spatial Interval: The samples are taken at intervals of .
Frequency Interval: The number of samples . The frequency interval is given by:
The discrete Fourier Transform of this signal will show a peak at 5 Hz, reflecting the original frequency of the signal. If we reduce to 0.05, increasing the sampling rate, the frequency interval would change to:
Thus, decreasing the spatial interval increases the frequency interval.
Practical Implications
Resolution and Detail:
In image processing, reducing the spatial sampling interval (e.g., increasing pixel resolution) allows capturing more detail but requires more storage and processing power. Conversely, increasing the sampling interval reduces the amount of detail, affecting the accuracy of frequency domain representations.Aliasing:
Insufficient sampling in the spatial domain causes aliasing, where high-frequency components appear as low-frequency components in the frequency domain, leading to distortion. This is why proper sampling is crucial to accurately capture and reconstruct signals or images.
Translation and Rotation
Translation and rotation are two fundamental geometric transformations used extensively in signal and image processing. These operations are essential for tasks such as object recognition, alignment, image registration, and pattern analysis. Understanding how translation and rotation affect signals and images in both the spatial and frequency domains is crucial for designing efficient algorithms in various applications.
1. Translation
Translation refers to shifting a signal or image in space without changing its shape or orientation. In mathematical terms, translating a 1D signal by a distance results in a new function:
For a 2D image , translation by distances and along the – and -axes respectively is given by:
Example:
Consider a 1D signal translated by .
- Original signal:
- Translated signal:
This translation shifts the sine wave two units to the right without altering its frequency or amplitude.
Effect of Translation in the Frequency Domain
In the frequency domain, translation introduces a phase shift but does not change the magnitude of the Fourier Transform. If is the Fourier Transform of , then the Fourier Transform of the translated function is given by:
For a 2D image, if is the Fourier Transform of , the transform of the translated image is:
Here, and represent phase shifts in the frequency domain, which correspond to the translations in the spatial domain.
2. Rotation
Rotation involves rotating a signal or image around a point, typically the origin. For a 2D image , rotating by an angle counterclockwise results in a new image defined by:
This transformation can be expressed as:
Example:
Consider a 2D image representing a simple geometric shape, such as a square centered at the origin. Rotating this image by would result in a square still centered at the origin, but with its sides now oriented diagonally.
Effect of Rotation in the Frequency Domain
Rotation in the spatial domain results in a corresponding rotation in the frequency domain. If is the Fourier Transform of the original image , the Fourier Transform of the rotated image will be:
where
This means the frequency components of the image are rotated by the same angle .
Practical Applications
Image Registration:
Translation and rotation are often used to align images taken at different times or from different viewpoints. Correcting for translation and rotation allows for accurate comparison and analysis.Pattern Recognition:
Objects in images may appear translated or rotated. Recognizing these transformations is essential for object detection and pattern matching.Image Compression and Filtering:
In some compression techniques, translating or rotating images to a standard orientation can simplify the processing and reduce data redundancy.
Periodicity
Periodicity is a fundamental concept in mathematics and signal processing, describing patterns that repeat over regular intervals. From the sine and cosine waves in trigonometry to the repeating patterns in signals and images, periodicity helps us analyze and understand the behavior of various functions and systems.
Mathematical Definition of Periodicity
A function is said to be periodic if there exists a positive number such that:
The smallest positive value of that satisfies this condition is called the fundamental period of the function.
Example 1: The Sine Function
The sine function, , is a classic example of a periodic function. Its fundamental period is because:
This property means that the sine wave repeats its values every units along the -axis.
Example 2: The Square Wave
A square wave is another periodic function, defined as:
repeating with period . For instance, if , then:
This means the square wave repeats every 2 units along the -axis.
Properties of Periodic Functions
Addition of Periodic Functions:
If and are two periodic functions with periods and , respectively, the sum is periodic if is a rational number. The period of will be the least common multiple (LCM) of and .Scaling and Shifting:
If is a periodic function with period , then is also periodic, where . The period of the scaled and shifted function is .Fourier Series Representation:
Any periodic function with period can be represented as a sum of sines and cosines, known as its Fourier series. This is a powerful tool for analyzing periodic functions in terms of their frequency components.
Periodicity in Discrete Signals
In discrete signals, periodicity plays a crucial role, especially in digital signal processing. A discrete signal is periodic if there exists a positive integer such that:
The smallest positive integer satisfying this condition is called the fundamental period of the discrete signal.
Example 3: Discrete Cosine Wave
Consider the discrete cosine wave .
This signal is periodic with a fundamental period of .
Periodicity in the Frequency Domain
Periodicity in the frequency domain is related to the spacing of spectral components in the discrete Fourier Transform (DFT). For a discrete signal of length , the DFT is periodic with period :
This property is essential in understanding how signals are represented in the frequency domain, particularly in applications such as digital filtering and spectral analysis.
Applications of Periodicity
Signal Analysis:
Periodic signals are fundamental in communications and signal processing, where they are used to represent repeating patterns, such as carrier waves and clock signals.Music and Acoustics:
Musical notes correspond to periodic sound waves. The fundamental frequency of these waves determines the pitch, while harmonics (higher frequencies) influence the timbre.Image Processing:
In images, periodicity can manifest as repeating patterns, textures, or grid structures. Detecting and analyzing these periodic patterns is essential for tasks like texture classification and image compression.Mechanical Systems:
In mechanical engineering, periodic functions describe oscillatory motions, such as the motion of a pendulum or the vibration of a spring.
Example: Fourier Series Representation
Consider the periodic square wave function defined earlier with period . Its Fourier series representation is given by:
This series expresses the square wave as a sum of sinusoidal components, demonstrating how even non-sinusoidal periodic functions can be broken down into basic sine and cosine functions.
Symmetry Properties
Symmetry is a fundamental concept in mathematics, physics, and various fields of engineering. It describes a situation where an object or function remains unchanged under certain transformations, such as reflection, rotation, or translation. Understanding symmetry properties helps simplify problems and reveal underlying patterns in complex systems.
Types of Symmetry
Reflection Symmetry (Mirror Symmetry)
A function or shape has reflection symmetry if it can be divided into two mirror-image halves. Mathematically, a function has reflection symmetry about the y-axis if:
This is also known as even symmetry.
Example:
The function is symmetric about the y-axis because .Rotational Symmetry
A function or shape has rotational symmetry if it looks the same after being rotated by a certain angle around a central point. A 2D function has rotational symmetry if it satisfies:
where are the coordinates obtained by rotating about the origin by an angle .
Example:
A circle centered at the origin is rotationally symmetric because it looks the same after any rotation about its center.Translational Symmetry
A function or shape has translational symmetry if it looks the same after being shifted by a certain distance. A function has translational symmetry if:
This is characteristic of periodic functions, where is the period.
Example:
The sine function, , has translational symmetry with period : .Rotoreflection Symmetry
A function or shape has rotoreflection symmetry if it remains unchanged under a combination of reflection and rotation. This type of symmetry is less common but is observed in some complex geometric shapes.
Symmetry in Mathematical Functions
Even and Odd Functions
- An even function satisfies . It is symmetric about the y-axis.
- An odd function satisfies . It is symmetric about the origin.
Examples:
- Even function: .
- Odd function: .
Symmetry in Trigonometric Functions
- The cosine function is an even function: .
- The sine function is an odd function: .
Symmetry in Complex Functions
For complex-valued functions, symmetry can be more intricate. A complex function (where ) might exhibit conjugate symmetry, where .
Symmetry in the Frequency Domain
In signal processing, symmetry properties in the frequency domain are essential for analyzing and simplifying signals.
Fourier Transform Symmetry:
- If a function is real and even, its Fourier Transform is also real and even.
- If is real and odd, then is imaginary and odd.
This property helps in reducing the computational complexity when analyzing signals.
Conjugate Symmetry of the Discrete Fourier Transform (DFT): For a real-valued discrete signal , the DFT exhibits conjugate symmetry:
where is the DFT of and is the length of the signal. This property allows us to reconstruct the entire frequency spectrum from half the DFT values.
Practical Applications of Symmetry
Physics and Chemistry: Symmetry principles are fundamental in physics and chemistry. For example, the symmetrical properties of molecules determine their chemical reactivity and physical properties. In physics, the conservation laws (like conservation of momentum) are closely related to symmetry properties.
Engineering and Design: In mechanical and civil engineering, symmetric structures are preferred for their stability and aesthetics. Symmetrical designs in architecture are not only visually appealing but also distribute loads more evenly.
Signal and Image Processing:
- Signal Analysis: Symmetry properties are used to simplify the analysis of signals and reduce the amount of data required for signal reconstruction.
- Image Processing: Symmetry detection in images is used for object recognition and classification. Symmetric objects are often easier to identify and analyze.
Computer Vision and Graphics: Symmetry is used in computer vision to recognize and track objects. In computer graphics, symmetric transformations are applied to generate realistic scenes and animations.
Example: Symmetry in Fourier Series
Consider a periodic function defined on . If is even, its Fourier series contains only cosine terms:
If is odd, the series contains only sine terms:
These properties simplify the computation of Fourier coefficients and the representation of the function.
Fourier Spectrum and Phase Angle
The Fourier Spectrum and Phase Angle are essential concepts in signal processing and analysis, offering insights into the frequency content and phase relationships within signals. By decomposing a signal into its constituent frequency components, the Fourier Transform allows us to represent and understand the signal in the frequency domain.
1. The Fourier Transform: A Brief Overview
The Fourier Transform converts a time-domain signal into its frequency-domain representation. For a continuous-time signal , the Fourier Transform is given by:
where:
- is the angular frequency in radians per second,
- is the imaginary unit, and
- is a complex function representing both amplitude and phase of each frequency component.
For discrete signals , the Discrete Fourier Transform (DFT) is used, defined as:
where:
- is the number of samples, and
- is the index corresponding to discrete frequency components.
2. Fourier Spectrum: Magnitude and Power Spectrum
The Fourier Spectrum provides a representation of the signal’s frequency content. It can be described in terms of the Magnitude Spectrum and the Power Spectrum.
(a) Magnitude Spectrum
The Magnitude Spectrum of is defined as the absolute value of the Fourier Transform:
where and are the real and imaginary parts of , respectively.
The Magnitude Spectrum indicates the amplitude of each frequency component present in the signal, without considering the phase information.
Example: Magnitude Spectrum of a Sine Wave
Consider a simple sine wave , where Hz.
- The Fourier Transform will show peaks at (i.e., rad/s).
- The Magnitude Spectrum will have spikes at these frequencies, indicating the presence of the 5 Hz component.
(b) Power Spectrum
The Power Spectrum represents the power distribution of the signal across different frequencies and is defined as the square of the Magnitude Spectrum:
The Power Spectrum is particularly useful for analyzing the energy content of signals in various frequency bands.
3. Phase Angle
The Phase Angle of gives the phase shift of each frequency component relative to the origin. It is calculated as:
The Phase Angle provides information on how the different frequency components are aligned in time.
Example: Phase Angle of a Cosine Wave
For a cosine wave , the Fourier Transform will show peaks at .
- The Phase Angle will be at these frequencies, indicating no phase shift, as the cosine wave is centered at the origin.
4. Interpretation of Magnitude and Phase
The complete Fourier representation of a signal consists of both its magnitude and phase information. Understanding both is crucial:
- The Magnitude Spectrum indicates the strength of each frequency component.
- The Phase Spectrum shows how these components are shifted in time relative to each other.
Reconstructing a signal from its Fourier Transform requires both the Magnitude and Phase Spectra. Ignoring phase information can lead to incorrect reconstruction, as phase determines the exact positioning of wave components in time.
5. Applications of Fourier Spectrum and Phase Angle
Signal Analysis and Filtering:
By analyzing the Fourier Spectrum, we can identify and isolate specific frequency components. This is useful in applications like noise reduction, where unwanted frequencies can be filtered out.Communications:
The phase information in modulated signals is crucial for demodulation. In phase modulation (PM) or phase-shift keying (PSK), the signal’s information is encoded in the phase angle.Image Processing:
The Fourier Transform is used to analyze the frequency content of images. High-frequency components correspond to edges, while low-frequency components correspond to smooth regions. The phase spectrum is essential for preserving image structures during transformations.Vibration Analysis:
In mechanical systems, analyzing the Magnitude and Phase Spectra of vibration signals can reveal resonant frequencies and help in diagnosing faults.
6. Example: Analyzing a Composite Signal
Consider a composite signal .
- The Magnitude Spectrum will show peaks at 5 Hz and 10 Hz.
- The Phase Spectrum will indicate a phase angle of for the sine component and for the cosine component.
This information helps us understand both the strength and the relative positioning of the frequency components in time.
7. Practical Considerations
Windowing and Leakage:
In practical applications, signals are often analyzed over finite time windows, which can introduce spectral leakage. Windowing functions, such as Hamming or Hanning windows, help reduce leakage and improve spectral estimates.Discrete vs. Continuous Fourier Transform:
The Discrete Fourier Transform (DFT) is used for digital signals, while the Continuous Fourier Transform applies to analog signals. The DFT is periodic, and its resolution depends on the length of the signal.Unwrapping the Phase:
The Phase Spectrum often appears discontinuous due to wrapping between and . Phase unwrapping algorithms are used to obtain a continuous phase representation, which is crucial for accurate analysis.
The 2-D Convolution Theorem
The 2-D Convolution Theorem is a powerful tool in image processing and signal analysis, simplifying the computation of convolution in the spatial domain by transforming it into multiplication in the frequency domain. This theorem provides an efficient way to perform operations like filtering, blurring, and edge detection in images.
1. Basics of 2-D Convolution
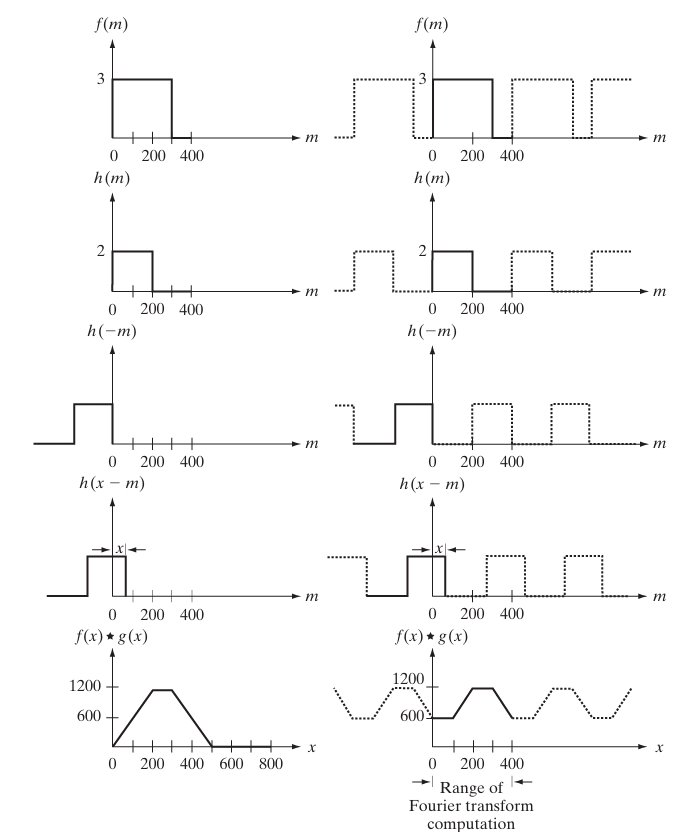
In the context of 2-D signals (such as images), the convolution of two functions and is defined as:
where:
- is the input function (e.g., an image).
- is the kernel or filter function.
- The operation denotes convolution.
This integral sums the product of the input function and the kernel function , considering all possible shifts .
Discrete 2-D Convolution
For digital images, the 2-D convolution is typically performed in the discrete domain. The discrete convolution of two functions and is given by:
This formula sums the product of the pixel values of and the shifted kernel over all possible shifts.
2. The 2-D Convolution Theorem
The 2-D Convolution Theorem states that the convolution of two functions in the spatial domain is equivalent to the multiplication of their Fourier Transforms in the frequency domain. Mathematically, if and are the 2-D Fourier Transforms of and respectively, then:
where represents the Fourier Transform of the convolution .
3. Proof of the 2-D Convolution Theorem
The proof of the 2-D Convolution Theorem involves the properties of the 2-D Fourier Transform. Let’s outline the key steps:
2-D Fourier Transform of Convolution:
By definition, the Fourier Transform of is:
Substitute the Convolution Definition:
Substitute the definition of into the above equation:
Interchange the Order of Integration:
We can interchange the order of integration since the integrals are over the entire space:
Simplify the Inner Integral:
The inner integral represents the Fourier Transform of the shifted kernel :
Therefore, we have:
Recognize the Fourier Transform of :
The integral now represents the Fourier Transform of , which is :
This completes the proof of the 2-D Convolution Theorem.
4. Practical Applications of the 2-D Convolution Theorem
Image Filtering and Smoothing:
Applying convolution in the spatial domain can be computationally intensive, especially for large images and kernels. By transforming both the image and the filter to the frequency domain, performing pointwise multiplication, and then applying the inverse Fourier Transform, we can achieve the same result more efficiently.
Example: Gaussian Blur
A Gaussian kernel can be used to blur an image. The Fourier Transform of a Gaussian function is also a Gaussian. By multiplying the Fourier Transform of the image with that of the Gaussian kernel and taking the inverse Fourier Transform, we can quickly apply a blur effect.
Edge Detection:
The convolution of an image with edge detection filters, like the Sobel or Laplacian filter, highlights areas of rapid intensity change. Using the Convolution Theorem, we can implement these operations in the frequency domain to improve performance.
Example: Sobel Filter
The Sobel filter emphasizes horizontal and vertical edges in an image. Convolving the image with the Sobel kernel in the spatial domain is equivalent to multiplying their Fourier Transforms in the frequency domain.
Pattern Matching and Template Matching:
The Convolution Theorem is used in template matching, where a template image is searched for within a larger image. By convolving the template with the image (or correlating them), we can identify regions in the image that match the template.
Image Reconstruction:
In applications such as computed tomography (CT) or magnetic resonance imaging (MRI), the Convolution Theorem helps in reconstructing images from their projections. By transforming the projection data to the frequency domain, performing necessary manipulations, and then transforming back to the spatial domain, accurate image reconstructions are possible.
5. Example: Applying the 2-D Convolution Theorem to Image Filtering
Consider an image represented by a function and a filter (kernel) represented by .
- Compute the 2-D Fourier Transforms and of the image and kernel, respectively.
- Multiply the transforms: .
- Apply the inverse 2-D Fourier Transform to obtain the filtered image: .
This method leverages the computational efficiency of Fourier Transforms, especially when using the Fast Fourier Transform (FFT) algorithm.
6. Computational Efficiency: Why Use the Convolution Theorem?
The direct convolution operation has a computational complexity of for an image of size and a kernel of size . Using the 2-D Convolution Theorem and the FFT, the complexity reduces to , which is significantly faster for large images and kernels.
References
- Oppenheim, A. V., & Schafer, R. W. (2010). Discrete-Time Signal Processing. Pearson.
- Gonzalez, R. C., & Woods, R. E. (2017). Digital Image Processing. Pearson.
- Bracewell, R. N. (1999). The Fourier Transform and Its Applications. McGraw-Hill.
