In image processing, the task of Representation and Description follows the segmentation of an image into regions, preparing the data for further analysis. Representation refers to the way a segmented region is depicted, which can focus either on the region’s external boundary or its internal characteristics. An external representation, emphasizing the boundary, is particularly useful when analyzing shape-related properties, as it captures the overall contour, orientation, and other boundary features of the region.
An internal representation, on the other hand, focuses on the region’s contents, such as color, texture, and pixel intensity patterns, providing insights into the internal structure. After choosing a representation, the next step is to describe the region with quantifiable features that make it meaningful for computer processing.
For example, if the region is represented by its boundary, it can be described by measuring boundary length, orientation, or the number of concavities—features that reveal shape characteristics. If represented by internal properties, it can be described by metrics like average color or texture, summarizing its internal composition. Regardless of the approach, descriptors are selected to be as invariant as possible to changes in size, translation, and rotation, ensuring consistency across varying conditions.
The choice between external and internal representation, or a combination of both, depends on the analysis focus. When shape is the primary interest, boundary representations are preferred, whereas internal representations are more relevant for surface properties. Ultimately, the goal of representation and description is to prepare segmented data for effective computational analysis, enabling deeper insights into the image’s regions.
Representation
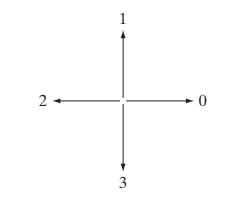
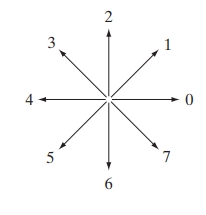
Representing the boundary of a region enables efficient shape analysis, storage, and comparison, which are critical for tasks like object recognition, tracking, and classification. Here, we discuss key techniques for representing boundaries, including Boundary Following, Chain Codes, Polygonal Approximations, Other Polygonal Approximations, and Signatures. Each topic is detailed with mathematical concepts and examples to illustrate the techniques.
1. Boundary (Border) Following
Boundary following, also known as border tracking or boundary extraction, is the process of identifying and recording the coordinates of pixels that make up the boundary of a shape in a binary image. For simplicity, binary images are used, where object pixels are labeled as 1 (foreground) and background pixels as 0.
Moore’s Boundary Tracing Algorithm
Moore’s algorithm is commonly used for boundary following due to its simplicity and effectiveness. It works as follows:
- Starting Point: Locate the first foreground pixel (labeled as 1) by scanning the image from the top-left corner. This becomes the initial boundary point.
- Neighbor Check: Starting from this point, check the 8-neighbors of the current pixel in a clockwise (or counterclockwise) order to find the next boundary pixel.
- Continue Until Loop Completes: Move to the next boundary pixel and repeat the process until the starting pixel is encountered again.
Mathematically, for a pixel at , if the neighbors are checked in clockwise order, the first neighboring pixel labeled 1 is added to the boundary sequence. This sequence of boundary points can be denoted as:
where is the starting point and each consecutive point belongs to the boundary of the shape.
Example: In a binary image with a square object, boundary following will produce an ordered list of points around the perimeter of the square. For a simple square with vertices at , boundary following would yield a sequence tracing around these points in order.
2. Chain Codes
Chain codes are a way to represent a boundary by encoding its direction of movement at each step. Typically, chain codes use either a 4-directional or 8-directional system to represent movement.
4-Directional and 8-Directional Chain Codes
- 4-Directional Chain Code: Uses directions {0, 1, 2, 3} to represent movement right, up, left, and down, respectively.
- 8-Directional Chain Code: Uses directions {0 to 7}, where each code represents one of eight possible moves around a pixel (right, up-right, up, up-left, left, down-left, down, down-right).
The chain code sequence for a boundary can be represented as:
where represents the direction of movement from one boundary point to the next.
Normalization of Chain Codes
Chain codes are sensitive to the starting point, so the first difference (difference between successive directions) is often used for rotation invariance. For example, given an 8-directional chain code, , the first difference is:
This difference is computed modulo 8 to ensure direction consistency, providing a rotation-invariant representation.
Example: For a square with vertices represented by movements: , the chain code is . The first difference for rotation invariance is , highlighting the repetitive and symmetrical nature of the square boundary.
3. Polygonal Approximations Using Minimum-Perimeter Polygons
Polygonal approximation aims to simplify complex boundaries by representing them with a minimum number of straight-line segments, ideally preserving the essential shape. The goal of Minimum-Perimeter Polygon (MPP) approximation is to capture the shape while reducing the number of points in the boundary.
Minimum-Perimeter Polygon (MPP) Algorithm
The MPP algorithm works by:
- Enclosing the Shape: Create a bounding box or set of cells around the shape boundary.
- Shrinking Boundary Points: “Shrink” or compress the boundary until a polygon with the smallest perimeter that encloses the shape is obtained.
- Selecting Vertices: Only keep boundary points that contribute to the shape’s essential features, minimizing the perimeter by using fewer points.
Mathematically, for a boundary , an MPP approximation minimizes the sum of distances between adjacent vertices:
where and are the points in the polygonal approximation of .
Example: For a complex shape like a star, the MPP will result in a polygon with vertices at the star’s tips and inner corners, approximating the shape while omitting intermediate points along each segment.
4. Other Polygonal Approximation Approaches
While MPP is effective, alternative methods for polygonal approximation also exist, such as merging and splitting techniques.
4.1 Merging Techniques
Merging techniques work by fitting lines to groups of boundary points, minimizing error iteratively:
- Error Minimization: Merge boundary points until the least-square error of the line fit exceeds a threshold.
- Segment Definition: Store each segment as part of the polygon approximation when it surpasses the error threshold.
Mathematically, the merging criterion involves finding line parameters and to minimize:
4.2 Splitting Techniques
Splitting methods subdivide a segment repeatedly until an error threshold is met:
- Initial Segments: Start with the longest segment between two extreme boundary points.
- Distance Threshold: If any intermediate point exceeds the perpendicular distance threshold from the segment, subdivide at that point.
Example: For an irregular shape, splitting may start with a segment connecting the two farthest boundary points, breaking it down iteratively to capture significant turns and corners.
5. Signatures
A signature is a one-dimensional (1D) representation of a boundary, which provides a compact form for comparison and analysis.
Centroid Distance Signature
One of the simplest forms is the centroid distance signature, where the distance from each boundary point to the centroid is computed and plotted as a function of the angle.
- Centroid Calculation: For a boundary , the centroid is:
- Distance Calculation: The distance from each boundary point to the centroid is:
- Signature Plot: Plot versus , the angle with respect to a reference direction.
Tangent Angle Signature
Another form of signature is the tangent angle signature, where the tangent angle at each point is plotted as a function of arc length along the boundary. If represents the arc length:
Example: For a circular boundary, the centroid distance signature is constant, while for an elongated ellipse, it shows a sinusoidal pattern, with peaks and troughs corresponding to the major and minor axes.
Boundary Descriptors
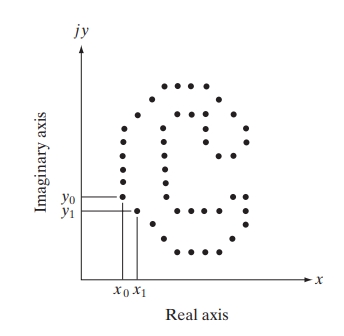
Boundary descriptors extract quantitative information from the shape of an object’s boundary, enabling comparison and classification. Key descriptors discussed here include Simple Descriptors, Shape Numbers, Fourier Descriptors, and Statistical Moments. Each topic is presented with mathematical concepts and examples.
1. Simple Descriptors
Simple descriptors are basic metrics that capture fundamental characteristics of a boundary, such as length, diameter, orientation, and curvature.
1.1 Length of a Boundary
The length of a boundary provides a basic measure of its perimeter. For a boundary represented by an ordered set of points , the length can be computed as:
This calculation sums up the Euclidean distances between consecutive boundary points.
Example: For a square with side length 4, represented by points at (0,0), (4,0), (4,4), and (0,4), the length is:
1.2 Diameter
The diameter of a boundary is defined as the maximum Euclidean distance between any two points on the boundary:
The diameter gives an indication of the object’s extent and is often aligned with the major axis of the shape.
Example: For a circular boundary with radius , the diameter is simply , as this is the maximum distance across the circle.
1.3 Curvature
Curvature is the rate of change of slope along the boundary, capturing how sharply the boundary bends at each point. For a boundary point , the curvature at that point can be estimated as:
where is the change in angle between two segments at point , and is the arc length between these points.
Curvature is useful for identifying corners and edges in a boundary. High curvature values often correspond to significant shape features, such as corners.
Example: For a triangle, the curvature is high at the vertices (corners) and zero along the straight edges.
2. Shape Numbers
Shape numbers are derived from chain-coded boundaries and provide a compact, rotation-invariant representation of a shape.
2.1 Chain Code and First Difference
A chain code represents a boundary as a sequence of directions. For a boundary represented in an 8-directional system, the chain code could be something like:
where each number represents a direction in the grid.
The first difference of a chain code sequence, defined as the difference between consecutive directions modulo 8, removes sensitivity to the starting point and provides rotation invariance. For the above chain code:
This difference sequence, or shape number, characterizes the shape without depending on its orientation in the image.
2.2 Order of a Shape Number
The order of a shape number is simply the length of the first difference sequence. A shape’s order is directly related to its complexity; for instance, a simple square would have a lower-order shape number than a complex star shape.
Example: For a square, the chain code might be repeated. The shape number’s first difference sequence is , with order 4, showing its rotational symmetry.
3. Fourier Descriptors
Fourier descriptors use the Fourier transform to represent boundary shapes in the frequency domain, capturing both global and local features.
3.1 Boundary Representation as a Complex Sequence
To apply Fourier descriptors, a boundary can be treated as a sequence of complex numbers. For a boundary with points , we define:
where and is the index of the boundary points.
3.2 Discrete Fourier Transform (DFT)
The Discrete Fourier Transform (DFT) of this complex sequence is:
where are the Fourier descriptors. These descriptors capture frequency components, with low-frequency terms representing the global shape and high-frequency terms representing finer details.
3.3 Reconstruction Using Fourier Descriptors
A boundary can be approximately reconstructed using only a subset of the Fourier descriptors:
where . This approximation captures the essential shape features, often with a substantial reduction in data.
Example: For a circular boundary with radius , only the first few Fourier descriptors are needed to reconstruct the circle accurately. Using all descriptors provides an exact reconstruction, but using fewer descriptors smooths out high-frequency variations, creating a simpler approximation.
4. Statistical Moments
Statistical moments are mathematical quantities that capture the distribution of points along a boundary, providing a summary of shape properties.
4.1 Basic Statistical Moments
For a boundary represented by points , the central moments of order are defined as:
where and are the centroid coordinates:
These moments summarize shape properties in terms of spatial distribution:
- : Variance along the x-axis, indicating horizontal spread.
- : Variance along the y-axis, indicating vertical spread.
- : Covariance, indicating the degree of elongation along the main diagonal.
4.2 Moment Invariants
Moment invariants are specific combinations of moments that remain constant under translation, rotation, and scaling. Hu’s moments are commonly used for boundary analysis:
These invariants provide robust shape descriptors, making them suitable for recognizing shapes regardless of orientation and size.
4.3 Example of Moment Calculation
Consider a boundary of an ellipse centered at with semi-axes and :
- Variance along major axis:
- Variance along minor axis:
- Moment Invariant: For an ellipse, Hu’s second moment invariant simplifies to reflect the aspect ratio, providing a unique descriptor for its shape.
Regional Descriptors
Regional Descriptors provide quantitative information about the internal properties of a region, beyond the boundary, enabling detailed analysis in applications like object recognition, image classification, and texture analysis. Here, we delve into four main types of regional descriptors: Simple Descriptors, Topological Descriptors, Texture, and Moment Invariants. Each section explores the relevant mathematical concepts and provides examples to illustrate the techniques.
1. Simple Descriptors
Simple descriptors summarize basic properties of a region, such as its area, center, orientation, and eccentricity. These descriptors are straightforward but form the foundation for more complex analysis.
1.1 Area
The area of a region represents the number of pixels within its boundary. For a binary image where the object pixels are labeled as 1 and the background as 0, the area can be calculated by summing the pixels inside the region:
where is 1 for object pixels and 0 for background pixels.
Example: In a binary image of a circle with radius , the area is approximately , assuming pixel resolution approximates the shape.
1.2 Centroid
The centroid (or center of mass) of a region is the average position of all its pixels and is given by:
where are the coordinates of the centroid.
Example: For a rectangular region, the centroid is located at the geometric center of the rectangle, at .
1.3 Eccentricity
Eccentricity is a measure of how elongated a region is. It is defined as the ratio of the distance between the foci of the ellipse that approximates the region to the length of its major axis. For an ellipse with semi-major axis and semi-minor axis , eccentricity is:
A circle has an eccentricity of 0, while a highly elongated shape has an eccentricity close to 1.
Example: A perfect circle has , and an elongated ellipse has approaching 1.
2. Topological Descriptors
Topological descriptors characterize the structural properties of a region that remain unchanged under continuous transformations (like stretching or bending). Common topological descriptors include connectivity, the Euler number, and the number of holes.
2.1 Connectivity
Connectivity refers to how pixels within a region are connected to each other. In binary images, pixels can be either 4-connected or 8-connected:
- 4-connected: A pixel is connected to its horizontal and vertical neighbors.
- 8-connected: A pixel is connected to its horizontal, vertical, and diagonal neighbors.
Connectivity is useful for identifying separate regions in an image.
2.2 Euler Number
The Euler number is a topological descriptor that quantifies the structure of a region by counting its connected components and holes:
where is the number of connected components, and is the number of holes.
Example: For an image with one solid object (C = 1) and no holes (H = 0), the Euler number . If the object has two holes, .
2.3 Number of Holes
The number of holes within a region is simply in the Euler formula. It represents internal areas not connected to the outer boundary, such as gaps or voids within an object.
Example: A ring-shaped object in a binary image has one connected component and one hole, giving .
3. Texture
Texture describes the spatial distribution of pixel intensities within a region, capturing patterns that can help differentiate objects. Various methods analyze texture, such as the Gray Level Co-occurrence Matrix (GLCM), statistical measures, and frequency-based methods.
3.1 Gray Level Co-occurrence Matrix (GLCM)
The GLCM captures how frequently pairs of pixel intensities (gray levels) occur at a specific spatial relationship within a region. Each element represents the frequency of pixel occurring adjacent to pixel . Common GLCM-based texture measures include:
- Contrast: Measures the intensity contrast between a pixel and its neighbor over the whole image.
- Homogeneity: Measures the closeness of the distribution of elements in the GLCM to the GLCM diagonal.
- Entropy: Measures the randomness of intensity distribution, higher for more complex textures.
Example: For a uniformly textured region, contrast and entropy are low, while homogeneity is high. A region with high variations in gray levels has high contrast and entropy.
3.2 Statistical Texture Measures
Statistical measures evaluate texture based on pixel intensity distributions:
- Mean : The average intensity of pixels in the region.
- Variance : Measures the spread of pixel intensities.
- Skewness: Indicates asymmetry in the pixel intensity distribution.
Example: A region with uniform pixel values has low variance, while a region with significant intensity changes has high variance.
4. Moment Invariants
Moment invariants are descriptors based on the spatial moments of a region, designed to be invariant to translation, rotation, and scaling, making them ideal for shape recognition.
4.1 Spatial Moments
For a 2D region represented by a binary image, the spatial moment of order is defined as:
where is 1 for pixels inside the region and 0 elsewhere.
Example: The zeroth moment gives the area of the region, and the first moments and help find the centroid.
4.2 Central Moments
Central moments are calculated relative to the centroid , making them translation-invariant:
where is given by:
4.3 Hu’s Moment Invariants
Hu’s moment invariants are specific combinations of central moments that remain constant under translation, scaling, and rotation. The first few Hu moment invariants are:
These invariants are calculated from normalized central moments, ensuring consistency regardless of object orientation or size.
Example: For a circle, Hu’s invariants yield specific values. When the circle is scaled, rotated, or shifted, the invariants remain unchanged, allowing it to be recognized across transformations.
References
- Sonka, M., Hlavac, V., & Boyle, R. (2014). Image Processing, Analysis, and Machine Vision. Cengage Learning.
- Gonzalez, R. C., & Woods, R. E. (2018). Digital Image Processing. Pearson.
- Szeliski, R. (2010). Computer Vision: Algorithms and Applications. Springer.
- Jain, A. K. (1989). Fundamentals of Digital Image Processing. Prentice Hall.
- Haralick, R. M., & Shapiro, L. G. (1992). Computer and Robot Vision. Addison-Wesley.
