Sampling and the Fourier Transform of Sampled Functions

The Fourier Transform is a powerful mathematical tool used to analyze signals in the frequency domain. When a continuous-time signal is sampled, the Fourier Transform of the sampled function introduces new characteristics that are crucial to understand in digital signal processing.

1. Continuous-Time Fourier Transform (CTFT)

Before diving into the Fourier Transform of sampled functions, let’s recall the Continuous-Time Fourier Transform (CTFT), which transforms a continuous-time signal $x(t)$ into its frequency-domain representation $X(f)$.

Mathematical Definition:

The CTFT of a signal $x(t)$ is given by the following integral:

where:

• $x(t)$ is the continuous-time signal,
• $f$ is the frequency in Hz,
• $j$ is the imaginary unit.

The inverse CTFT is used to reconstruct the time-domain signal from its frequency components:

2. Sampling of Continuous-Time Signals

When a continuous-time signal is sampled, it is multiplied by a sampling function or a Dirac comb, which is a train of equally spaced delta functions. The result of this multiplication is a discrete-time signal, represented as a series of samples.

Mathematical Expression:

Let $x(t)$ be a continuous-time signal, and let the signal be sampled at intervals of $T_s$ seconds, where $T_s$ is the sampling period. The sampling function $S(t)$ is:

The sampled signal $x_s(t)$ is:

This multiplication picks out the values of $x(t)$ at the sampling instants $t = nT_s$.

3. Fourier Transform of Sampled Signals

To understand how sampling affects the frequency content of the signal, we take the Fourier Transform of the sampled signal.

Fourier Transform of the Sampling Function:

The Fourier Transform of the sampling function $S(t)$ is a Dirac comb in the frequency domain, which can be expressed as:

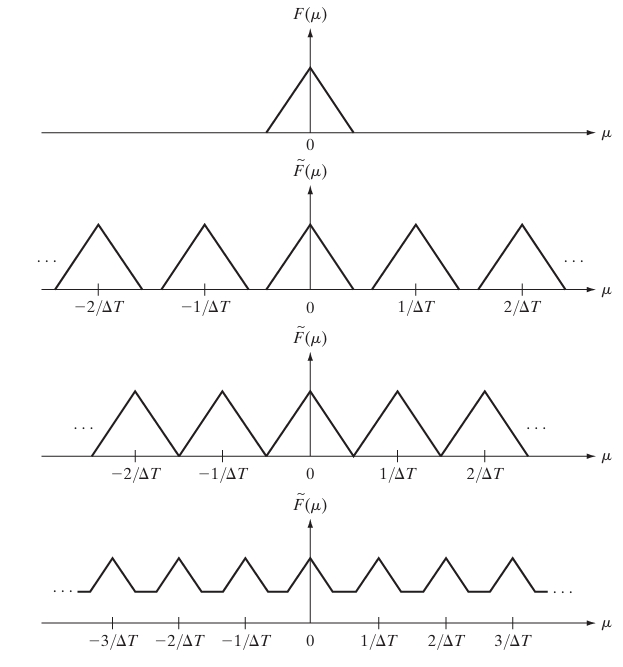
where $f_s = \frac{1}{T_s}$ is the sampling frequency. This indicates that sampling introduces periodic repetitions of the signal’s spectrum, spaced at intervals of $f_s$.

Fourier Transform of the Sampled Signal:

The Fourier Transform of the sampled signal $x_s(t)$ is given by:

Using the convolution theorem, the Fourier Transform of the product of two functions (here, $x(t)$ and $S(t)$) is the convolution of their individual Fourier Transforms. Therefore:

This means that the Fourier Transform of the sampled signal is the original Fourier Transform $X(f)$, replicated periodically at intervals of $f_s$. Mathematically:

Key Points:

• Periodic Replication: Sampling a signal in the time domain leads to periodic replication of its spectrum in the frequency domain.
• Aliasing: If the signal contains frequencies higher than $\frac{f_s}{2}$, the replicated spectra will overlap, causing aliasing. This results in distortion in the sampled signal’s frequency representation.

4. Nyquist Criterion and Aliasing

To avoid aliasing, the Nyquist Criterion must be satisfied. This criterion states that the sampling frequency $f_s$ must be at least twice the highest frequency component $f_{\text{max}}$ in the original signal:

If the signal is sampled at a frequency lower than this Nyquist rate, high-frequency components will “fold” into lower frequencies, resulting in aliasing.

Example of Aliasing:

Consider a continuous signal with frequency components up to 1 kHz. According to the Nyquist criterion, the sampling frequency must be at least:

If the signal is sampled at 1500 Hz (below the Nyquist rate), frequencies above 750 Hz will alias, causing distortion.

5. Reconstruction of the Original Signal

If the signal is sampled according to the Nyquist rate, it is possible to reconstruct the original continuous-time signal from its samples using a reconstruction filter.

Reconstruction Process:

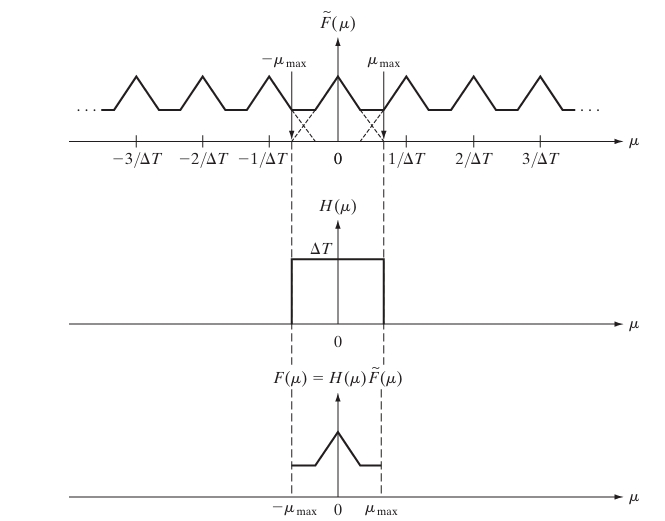
The Fourier Transform of the sampled signal consists of repeated copies of the original spectrum $X(f)$. To recover the original signal, we apply a low-pass filter that removes the higher-frequency copies and keeps only the original spectrum within the range $[-f_s/2, f_s/2]$. After filtering, the inverse Fourier Transform is applied to return to the time domain.

Mathematically:

The reconstructed signal $x(t)$ is:

where $\text{sinc}(t) = \frac{\sin(\pi t)}{\pi t}$ is the sinc function, acting as the interpolation kernel.

6. Example: Fourier Transform of a Sampled Sine Wave

Consider a continuous-time sine wave signal:

where $f_0 = 100 \, \text{Hz}$.

If we sample this signal at a rate $f_s = 500 \, \text{Hz}$, the sampling period is $T_s = \frac{1}{f_s} = 0.002 \, \text{seconds}$. The sampled signal is:

Now, let’s examine the Fourier Transform of the sampled signal. The Fourier Transform of the continuous signal $x(t)$ is:

After sampling, the Fourier Transform of the sampled signal becomes:

For $f_0 = 100 \, \text{Hz}$ and $f_s = 500 \, \text{Hz}$, the spectrum contains copies of $X(f)$ at intervals of $500 \, \text{Hz}$, i.e., at $\pm 100 \, \text{Hz}, \pm 500 \, \text{Hz}, \pm 900 \, \text{Hz}, \dots$.

If the signal is sampled at $f_s = 200 \, \text{Hz}$, which is less than the Nyquist rate, aliasing occurs. Frequencies above 100 Hz will fold back into the lower frequencies, causing distortion in the sampled signal.

The Sampling Theorem, also known as the Nyquist-Shannon Sampling Theorem, is a fundamental principle in the field of signal processing. It defines the conditions under which a continuous-time signal can be completely represented and reconstructed from its discrete samples without any loss of information. This theorem is essential for ensuring accurate digital representation of analog signals.

1. Statement of the Sampling Theorem

If a continuous-time signal $x(t)$ is band-limited (i.e., its Fourier Transform $X(f)$ is zero for all frequencies greater than a certain maximum frequency $f_{\text{max}}$), the signal can be exactly reconstructed from its samples if the sampling frequency $f_s$ satisfies the following condition:

This minimum required sampling rate $f_s = 2 f_{\text{max}}$ is called the Nyquist rate.

2. Intuition Behind the Sampling Theorem

The sampling theorem tells us that in order to capture all the information present in a signal, the sampling rate must be at least twice the highest frequency present in the signal. If the signal is sampled at a lower rate than the Nyquist rate, aliasing occurs, resulting in distortions and loss of information.

Key Concepts:

• Band-Limited Signal: A signal is said to be band-limited if its frequency components are confined to a certain finite range. In other words, the signal’s Fourier Transform $X(f)$ is zero for $|f| > f_{\text{max}}$.

• Nyquist Rate: The minimum sampling rate, which is twice the maximum frequency component $f_{\text{max}}$ in the signal, is called the Nyquist rate.

• Aliasing: If the sampling frequency is lower than the Nyquist rate, the high-frequency components of the signal will appear as lower frequencies in the sampled signal. This effect is known as aliasing.

3. Mathematical Proof of the Sampling Theorem

To understand the theorem, let’s examine it mathematically using the Fourier Transform.

Continuous-Time Signal:

Let $x(t)$ be a continuous-time signal with a Fourier Transform $X(f)$. Assume that $x(t)$ is band-limited, meaning $X(f) = 0$ for $|f| > f_{\text{max}}$.

Sampled Signal:

When the signal is sampled at intervals of $T_s$ (sampling period), the discrete-time signal is:

where $T_s = \frac{1}{f_s}$ is the sampling period, and $f_s$ is the sampling frequency.

The Fourier Transform of the sampled signal is:

This equation shows that the spectrum of the sampled signal is a periodic repetition of the original signal’s spectrum, spaced at intervals of $f_s$.

Condition for Perfect Reconstruction:

For perfect reconstruction of the original signal, the spectra copies must not overlap. This happens if the sampling frequency satisfies:

If $f_s$ is less than $2f_{\text{max}}$, the spectra will overlap, leading to aliasing, which distorts the signal and makes it impossible to recover the original signal.

4. Aliasing: The Effect of Undersampling

When the sampling frequency $f_s$ is lower than the Nyquist rate, high-frequency components of the signal will fold into the lower frequency range, causing aliasing. Aliasing makes the reconstructed signal inaccurate because the frequency components become indistinguishable.

Aliasing Example:

Consider a continuous-time sine wave $x(t) = \sin(2\pi f_0 t)$, where $f_0 = 1 \, \text{kHz}$. If this signal is sampled at a frequency $f_s = 1.5 \, \text{kHz}$, the sampling rate is below the Nyquist rate $f_s = 2f_0 = 2 \, \text{kHz}$. As a result, aliasing occurs, and the signal will appear as if it has a lower frequency component, $f_{\text{alias}}$, given by:

In this case:

Thus, the 1 kHz signal is aliased and will appear as a 500 Hz signal after sampling.

5. Reconstruction of the Original Signal

If the signal is sampled at or above the Nyquist rate, the original signal can be perfectly reconstructed from its discrete samples. The process involves passing the sampled signal through an ideal low-pass filter that removes the replicated spectra and retains only the frequency components within the range $[-f_s/2, f_s/2]$.

Reconstruction Formula:

The reconstructed signal $x(t)$ can be expressed as:

where $x[n] = x(nT_s)$ are the discrete samples, and the sinc function is defined as:

The sinc function acts as an interpolation kernel that reconstructs the continuous-time signal from its discrete samples.

6. Practical Considerations

In practice, signals may not always be perfectly band-limited, and it can be difficult to achieve ideal sampling conditions. To mitigate aliasing in real-world systems, some additional techniques are employed:

• Anti-Aliasing Filter: Before sampling, an anti-aliasing filter (usually a low-pass filter) is applied to the continuous signal to remove frequency components higher than $f_s/2$. This ensures that the sampled signal meets the conditions of the sampling theorem.

• Oversampling: In some applications, signals are sampled at rates significantly higher than the Nyquist rate. This is known as oversampling and is used to simplify the design of filters and reduce aliasing.

7. Example: Applying the Sampling Theorem

Let’s consider a real-world example of a signal with frequency components up to 1 kHz. According to the Nyquist-Shannon sampling theorem, the minimum sampling frequency required is:

Thus, a sampling rate of at least 2 kHz is required to capture all the information from the signal. If we sample at this rate, the signal can be perfectly reconstructed using interpolation.

Undersampling Example:

If the same signal is sampled at 1.5 kHz (below the Nyquist rate), the frequencies above 750 Hz will alias and appear as lower frequencies in the sampled signal, causing distortion and making perfect reconstruction impossible.

Aliasing is a phenomenon that occurs in digital signal processing when a continuous-time signal is sampled at a rate lower than the Nyquist rate. This results in the overlap of signal frequencies, which causes high-frequency components to “fold” into lower frequencies, distorting the original signal’s representation in the digital domain.

1. Understanding Aliasing

Aliasing happens when a signal is sampled at a rate insufficient to capture all of its frequency components accurately. In such cases, different frequency components in the original signal can become indistinguishable after sampling, and the sampled signal can have a distorted or misleading frequency content.

Key Concepts:

• Nyquist Rate: The minimum sampling frequency needed to avoid aliasing is twice the highest frequency component in the original signal. This is known as the Nyquist rate, denoted by $f_s$.

• Folding of Frequencies: When a signal is undersampled, higher-frequency components “fold” back into the lower-frequency range, making them indistinguishable from the lower-frequency components.

2. Mathematical Concept of Aliasing

To explore aliasing mathematically, let’s start with the concept of sampling. When a continuous-time signal $x(t)$ is sampled at intervals of $T_s$, we get a discrete-time signal represented as:

where:

• $T_s = \frac{1}{f_s}$ is the sampling period,
• $f_s$ is the sampling frequency,
• $\delta(t – nT_s)$ is the Dirac delta function.

The Fourier Transform of the sampled signal $x_s(t)$ is:

This equation indicates that the frequency spectrum of the sampled signal consists of periodic repetitions of the original signal’s spectrum $X(f)$, shifted by multiples of the sampling frequency $f_s$.

Condition for No Aliasing:

To prevent the overlapping of these repeated spectra, the sampling frequency must satisfy the Nyquist criterion:

where $f_{\text{max}}$ is the highest frequency component of the signal. If this condition is met, the spectra will remain separated, and the original signal can be recovered without distortion.

Aliasing Effect:

When the sampling frequency $f_s$ is less than $2f_{\text{max}}$, the repeated spectra overlap, and high-frequency components fold into the lower frequency range. This folding of frequencies results in aliasing, and the signal becomes distorted because different frequencies become indistinguishable.

3. Folding Frequency and Aliased Frequencies

Let’s assume that the original continuous signal has a frequency $f_0$ higher than half the sampling rate. After sampling, the observed frequency will be:

where $N$ is an integer such that $f_{\text{alias}}$ falls within the frequency range $[0, f_s/2]$. This is the folding frequency, and it determines the aliased frequency, which is the lower frequency that appears in the sampled signal instead of the original high frequency.

4. Aliasing Example

Let’s take an example of a continuous sine wave signal $x(t)$ with frequency $f_0 = 1 \, \text{kHz}$:

Case 1: Sampling at Nyquist Rate

If the signal is sampled at the Nyquist rate $f_s = 2f_0 = 2 \, \text{kHz}$, the sampling period is:

The sampled signal will retain its original frequency, and no aliasing will occur.

Case 2: Undersampling

Now, let’s consider the case where the sampling rate is $f_s = 1.5 \, \text{kHz}$, which is below the Nyquist rate:

In this case, the original frequency $f_0 = 1 \, \text{kHz}$ exceeds half the sampling frequency $f_s/2 = 750 \, \text{Hz}$. As a result, the frequency $f_0$ will fold into the lower range.

Using the aliasing formula:

For $N = 1$:

Thus, after sampling, the signal appears to have a frequency of 500 Hz instead of 1 kHz. This distortion is the result of aliasing, where the original high frequency “folds” into a lower frequency.

5. Graphical Representation of Aliasing

Aliasing can also be understood visually by examining the frequency domain. Consider a band-limited signal with a spectrum that spans from $-f_{\text{max}}$ to $f_{\text{max}}$. When the signal is sampled at a rate lower than the Nyquist rate, the repeated copies of the spectrum overlap, causing the high-frequency components to fold back into the lower frequency range.

Frequency Spectrum Without Aliasing:

When the sampling rate is sufficient ($f_s \geq 2f_{\text{max}}$), the frequency spectrum looks like this:

And the replicated spectra are spaced at $\pm f_s, \pm 2f_s, \ldots$, but remain non-overlapping.

Frequency Spectrum With Aliasing:

When the sampling rate is too low ($f_s < 2f_{\text{max}}$), the repeated spectra overlap, leading to aliasing:

In the overlapping regions, the high-frequency components are indistinguishable from the lower frequencies, leading to distorted frequency content in the sampled signal.

6. Prevention of Aliasing

Aliasing can be prevented by ensuring that the sampling rate meets or exceeds the Nyquist rate. However, in practical applications, it’s not always possible to know the highest frequency component of a signal. To address this, the following techniques are used:

Anti-Aliasing Filter:

An anti-aliasing filter is a low-pass filter applied to the signal before sampling to remove any frequency components above $f_s/2$. By filtering out high-frequency components, the filter ensures that the signal is band-limited to below the Nyquist frequency, preventing aliasing.

Oversampling:

In many applications, signals are sampled at rates much higher than the Nyquist rate. This technique is called oversampling and helps reduce the impact of aliasing while simplifying filter design.

7. Real-World Example: Audio Sampling

In audio processing, aliasing can cause significant distortion in sound quality. For example, the human ear can hear frequencies up to about 20 kHz. According to the Nyquist theorem, the minimum sampling rate for recording audio without aliasing must be at least:

In practice, the standard sampling rate for high-quality audio is 44.1 kHz (as used in CDs), ensuring that all audible frequencies are captured accurately without aliasing. If the sampling rate were lower than 40 kHz, high-pitched sounds above 20 kHz would alias and create distorted, low-frequency noise in the recording.