Sharpening Spatial Filters

The principal objective of sharpening is to highlight transitions in intensity. uses of image sharpening vary and include applications ranging from electronic printing and medical imaging to industrial inspection and autonomous guidance in military systems.

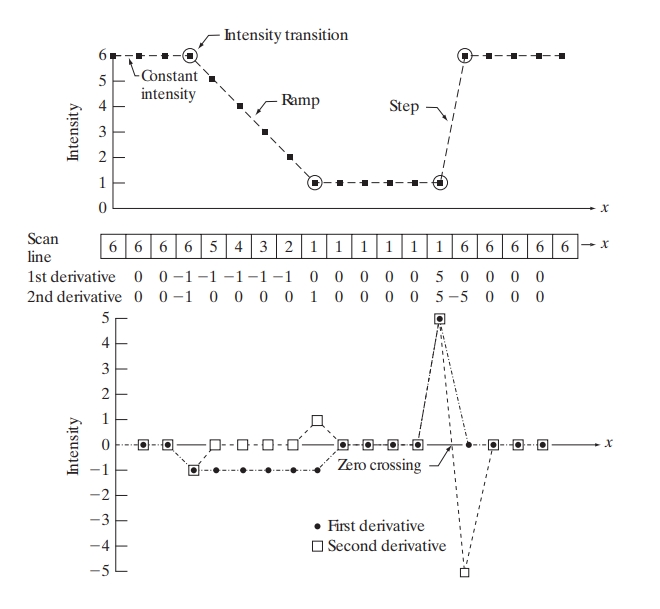
Fundamentally, the strength of the response of a derivative operator is proportional to the degree of intensity discontinuity of the image at the point where the operator is applied. Consequently, image differentiation enhances edges and other discontinuities (such as noise) while deemphasizing areas with slowly varying intensities.

Table of Contents

Sharpening Spatial Filters: An In-Depth Analysis

Spatial filtering is a critical technique in image processing used to manipulate or enhance images by applying various operations to the pixel values. Sharpening spatial filters are particularly significant as they enhance the edges and fine details in an image, making the image appear clearer and more defined.

1. Fundamentals of Spatial Filtering

Spatial filtering involves the convolution of an image with a filter mask (also called a kernel). The filter mask is a small matrix that slides over the image, performing element-wise multiplication and summing the results to produce a new pixel value. Mathematically, this operation can be described as:

$g(x, y) = \sum_{i=-k}^{k} \sum_{j=-k}^{k} f(x+i, y+j) \cdot h(i, j)$

where:

$g(x, y)$ is the filtered image.
$f(x, y)$ is the original image.
$h(i, j)$ is the filter mask.
$k$ is the size of the filter mask (usually $k = \frac{N-1}{2}$ for an $N \times N$ mask).

2. Sharpening Filters

Sharpening filters highlight the edges in an image by amplifying high-frequency components. These filters work by emphasizing the intensity difference between adjacent pixels, which is crucial for edge detection and image enhancement.

2.1. High-Pass Filters

High-pass filters allow high-frequency components to pass through while attenuating low-frequency components. One of the simplest high-pass filters is the Laplacian filter, which can be represented as:

$h = \begin{bmatrix} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \end{bmatrix}$

The Laplacian filter enhances edges by computing the second-order derivative of the image. The convolution operation with this filter can be expressed as:

$g(x, y) = \left[ f(x, y) * \begin{bmatrix} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \end{bmatrix} \right]$

2.2. Unsharp Masking

Unsharp masking is another popular technique for image sharpening. It involves the following steps:

Blur the original image to remove high-frequency noise.
Subtract the blurred image from the original image to get the mask.
Add the mask to the original image to obtain the sharpened image.

Mathematically, the process can be described as:

$f_{\text{blurred}}(x, y) = f(x, y) * h_{\text{blur}}$ $m(x, y) = f(x, y) – f_{\text{blurred}}(x, y)$ $g(x, y) = f(x, y) + k \cdot m(x, y)$

where:

$h_{\text{blur}}$ is a low-pass filter (e.g., Gaussian filter).
$m(x, y)$ is the mask.
$k$ is a scaling factor (usually $k = 1$ ).

3. Derivative-Based Filters

Derivative-based filters, such as gradient filters, play a crucial role in image sharpening. These filters use derivatives to detect edges by identifying areas with significant intensity changes.

3.1. First-Order Derivatives

First-order derivatives measure the rate of change in intensity. In a discrete image, the first-order derivative can be approximated using difference equations. The simplest first-order derivative filters are the Roberts Cross operator, the Prewitt filter, and the Sobel filter.

Roberts Cross Operator:

$G_x = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}, \quad G_y = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}$

Prewitt Filter:

$G_x = \begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \end{bmatrix}, \quad G_y = \begin{bmatrix} -1 & -1 & -1 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \end{bmatrix}$

Sobel Filter:

$G_x = \begin{bmatrix} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{bmatrix}, \quad G_y = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ 1 & 2 & 1 \end{bmatrix}$

The gradient magnitude is given by:

$g(x, y) = \sqrt{(f(x, y) * G_x)^2 + (f(x, y) * G_y)^2}$

3.2. Second-Order Derivatives

Second-order derivatives measure the rate of change of the first derivative, providing a more pronounced response to edges. The Laplacian filter, which computes the sum of the second-order derivatives in the x and y directions, is a widely used second-order derivative filter.

The Laplacian operator can be approximated as:

$\nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}$

Using discrete approximations, the Laplacian filter can be represented by various masks, including:

$h = \begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix} \quad \text{or} \quad h = \begin{bmatrix} 1 & 1 & 1 \\ 1 & -8 & 1 \\ 1 & 1 & 1 \end{bmatrix}$

4. Frequency Domain Approach

In addition to spatial domain methods, sharpening can also be performed in the frequency domain. This involves transforming the image using the Fourier Transform, manipulating the frequency components, and then transforming back to the spatial domain.

The Fourier Transform of an image $f(x, y)$ is:

$F(u, v) = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) e^{-j2\pi\left( \frac{ux}{M} + \frac{vy}{N} \right)}$

A high-pass filter in the frequency domain can be applied by multiplying the Fourier-transformed image with a high-pass mask $H(u, v)$ :

$G(u, v) = F(u, v) \cdot H(u, v)$

Common high-pass masks include the ideal high-pass filter, Butterworth high-pass filter, and Gaussian high-pass filter. After applying the filter, the inverse Fourier Transform is used to obtain the sharpened image:

$g(x, y) = \text{IFT}(G(u, v))$

5. Practical Considerations

5.1. Noise Amplification

Sharpening filters, particularly those that enhance high-frequency components, can also amplify noise. To mitigate this, it is essential to preprocess the image using noise reduction techniques before applying sharpening filters.

5.2. Boundary Effects

When applying convolution, boundary effects can occur where the filter extends beyond the image boundaries. Techniques such as padding (zero-padding, replicating edge pixels, etc.) are used to address these issues.

5.3. Parameter Selection

Choosing appropriate filter parameters (e.g., the scaling factor $k$ in unsharp masking) is crucial for obtaining the desired sharpening effect without introducing artifacts.

Conclusion

Sharpening spatial filters play a vital role in enhancing image details and making edges more prominent. Understanding the mathematical principles behind these filters, including derivatives, allows for more effective implementation and optimization. Whether using high-pass filters, gradient-based methods, or frequency domain techniques, careful consideration of noise and boundary effects is essential for achieving high-quality results. As image processing technology continues to advance, sharpening filters will remain a cornerstone of various applications, from photography to medical imaging.