Some Basic Relationships between Pixels

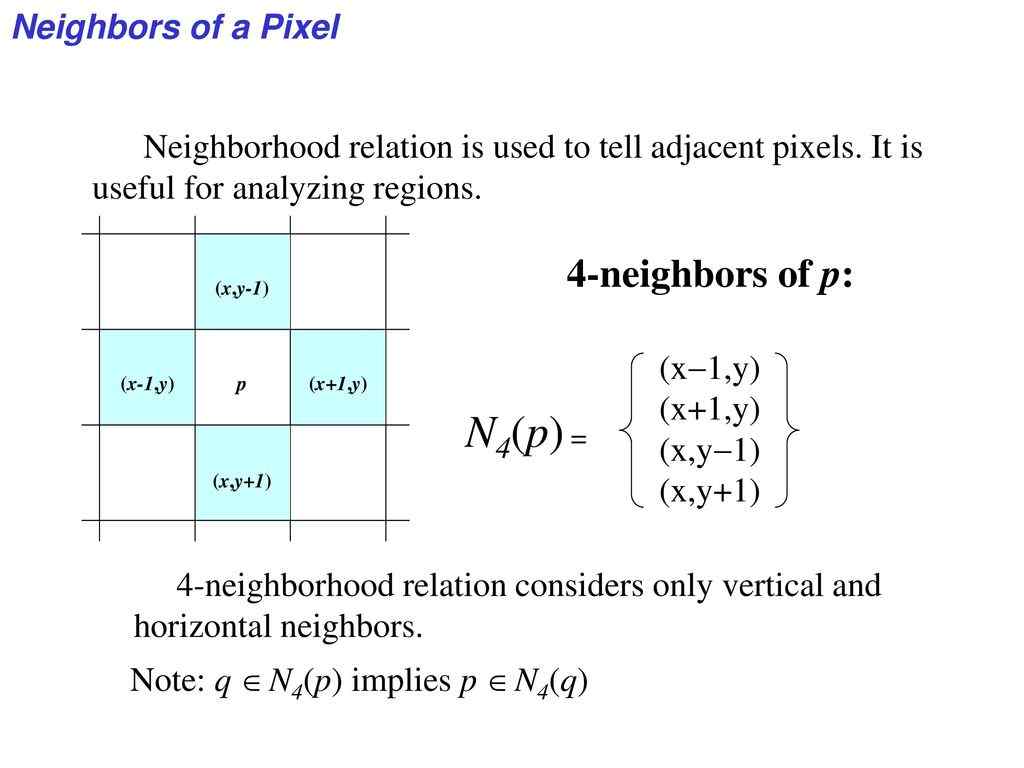
A pixel $p$ at coordinates $(x, y)$ has four horizontal and vertical neighbors whose coordinates are given by:

• $(x – 1, y)$ (left neighbor)
• $(x + 1, y)$ (right neighbor)
• $(x, y – 1)$ (top neighbor)
• $(x, y + 1)$ (bottom neighbor)

This set of pixels, known as the 4-neighbors of $p$, is denoted by $N_4(p)$. Each pixel is a unit distance from $p$, and some of the neighbor locations of $p$ may lie outside the digital image if $p$ is on the border of the image. Strategies for handling this issue are discussed in Chapter 3.

The four diagonal neighbors of $p$ have coordinates:

• $(x – 1, y – 1)$ (top-left neighbor)
• $(x + 1, y – 1)$ (top-right neighbor)
• $(x – 1, y + 1)$ (bottom-left neighbor)
• $(x + 1, y + 1)$ (bottom-right neighbor)

These points, along with the 4-neighbors, are collectively called the 8-neighbors of $p$, denoted by $N_8(p)$. Similar to the 4-neighbors, some of the neighbor locations in $N_8(p)$ may fall outside the image if $p$ is on the border of the image.

In the context of digital image processing, the concept of adjacency refers to the relationship between pixels based on their spatial positions and intensity values. Let’s break down the explanation provided:

1. Definition of Intensity Value Set (V):

   • The set $V$ represents the intensity values used to define adjacency.
   • In a binary image, where pixels have values of either 0 or 1, adjacency typically refers to pixels with a value of 1.
   • In a grayscale image, $V$ contains a range of intensity values (e.g., 0 to 255).

2. Types of Adjacency: a. 4-Adjacency: Two pixels $p$ and $q$ are considered 4-adjacent if $q$ is in the set $V$ and is located horizontally or vertically adjacent to $p$. b. 8-Adjacency: Two pixels $p$ and $q$ are considered 8-adjacent if $q$ is in the set $V$ and is located in any of the eight neighboring positions around $p$ (horizontally, vertically, or diagonally). c. m-Adjacency (Mixed Adjacency):

   • Two pixels $p$ and $q$ are considered m-adjacent if either of the following conditions is met: (i) $q$ is in the set $V$. (ii) $q$ is in the set $V$ and there are no pixels in the set $V$ along the path from $p$ to $q$.

For pixels $p$, $q$, and $z$, with coordinates $(x, y)$, $(s, t)$, and $(v, w)$ respectively, $D$ is considered a distance function or metric if:

(a) Non-negativity: $D(p, q) \geq 0$ for all $p$ and $q$.

(b) Identity of Indiscernibles: $D(p, q) = 0$ if and only if $p = q$.

(c) Symmetry: $D(p, q) = D(q, p)$ for all $p$ and $q$.

The Euclidean distance between pixels $p$ and $q$ is defined as:

$D_{\text{Euclidean}}(p, q) = \sqrt{(x – s)^2 + (y – t)^2}$

For this distance measure, the pixels within a distance $r$ from $(x, y)$ are the points contained within a disk of radius $r$ centered at $(x, y)$.

The distance, also known as the city-block distance, between pixels $p$ and $q$ is defined as:

$D_{\text{City-Block}}(p, q) = |x – s| + |y – t|$

In this scenario, the pixels within a distance $r$ from $(x, y)$ form a diamond centered at $(x, y)$. For example, the pixels with a distance of $r$ from $(x, y)$ form the contours of constant distance.

The distance, referred to as the chessboard distance, between pixels $p$ and $q$ is defined as:

$D_{\text{Chessboard}}(p, q) = \max(|x – s|, |y – t|)$

In this case, the pixels within a distance $r$ from $(x, y)$ form a square centered at $(x, y)$. For example, the pixels with a distance of $r$ from $(x, y)$ form the contours of constant distance.

Note that the $D_4$ and $D_8$ distances between $p$ and $q$ are independent of any paths between the points since they solely rely on the coordinates of the points. However, if considering m-adjacency, the distance between two points is defined as the shortest m-path between them. In such cases, the distance between two pixels depends on the values of the pixels along the path and their neighbors.