The Basics of Filtering in the Frequency Domain

by

Filtering is a fundamental concept in signal processing, used to enhance or suppress specific features within a signal. While filters can be applied directly in the time domain, there is a powerful alternative approach: filtering in the frequency domain. This method leverages the properties of the Fourier Transform to manipulate the frequency components of a signal, allowing for more precise control over its spectral content. By transforming a signal from the time domain to the frequency domain, we can isolate and modify specific frequency bands with greater accuracy. This introduction explores the core principles of frequency-domain filtering, its advantages, and common applications, laying the groundwork for a deeper understanding of how signals can be effectively processed and analyzed using this technique.

Additional Characteristics of the Frequency Domain

The frequency domain offers a unique perspective on signal processing, providing insights that are not always apparent in the time domain. By representing signals in terms of their frequency components, we can analyze and manipulate their spectral properties more effectively.

1. Magnitude and Phase Spectrum

In the frequency domain, a signal is represented by its Fourier Transform, which decomposes it into a series of sinusoids of different frequencies. The Fourier Transform X(f)X(f) of a time-domain signal x(t)x(t) is given by:

X(f)=∫−∞∞x(t)e−j2πft dtX(f) = \int_{-\infty}^{\infty} x(t) e^{-j2\pi ft} \, dt

The result, X(f)X(f), is a complex function with both magnitude and phase. The magnitude spectrum ∣X(f)∣|X(f)| shows the amplitude of the frequency components, while the phase spectrum arg⁡(X(f))\arg(X(f)) represents their phase shifts.

Example:

Consider a simple time-domain signal:

x(t)=cos⁡(2πf1t)+cos⁡(2πf2t)x(t) = \cos(2\pi f_1 t) + \cos(2\pi f_2 t)

where f1=5f_1 = 5 Hz and f2=10f_2 = 10 Hz. Its Fourier Transform X(f)X(f) will have two spikes at f1=5f_1 = 5 Hz and f2=10f_2 = 10 Hz in the magnitude spectrum, indicating the presence of these frequencies in the signal.

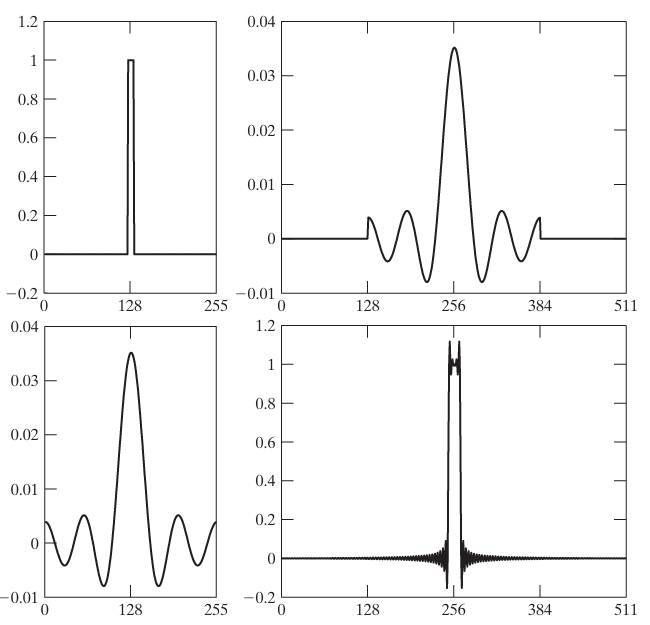
2. Spectral Leakage

Spectral leakage occurs when a signal’s frequency content spreads into adjacent frequency bins, typically due to the finite length of the signal or the choice of windowing function. It can distort the frequency representation, making it difficult to accurately interpret the spectrum.

Mathematical Explanation:

For a discrete-time signal x[n]x[n] of length NN, the Discrete Fourier Transform (DFT) is defined as:

X[k]=∑n=0N−1x[n]e−j2πknNX[k] = \sum_{n=0}^{N-1} x[n] e^{-j2\pi \frac{kn}{N}}

If the signal is not periodic within the window NN, the resulting frequency components are spread, causing leakage. This effect can be visualized by applying a rectangular window to a sinusoidal signal and observing the side lobes in its frequency spectrum.

Example:

Suppose x[n]=cos⁡(2π532n)x[n] = \cos(2\pi \frac{5}{32} n) for n=0,1,…,31n = 0, 1, \ldots, 31. The signal has a frequency component at 5/32 cycles per sample. If we compute its DFT, we observe leakage around the main frequency component, indicating the spread into adjacent frequency bins.

3. Windowing and Its Impact

To mitigate spectral leakage, windowing functions like Hamming, Hanning, and Blackman are applied to the signal before computing the Fourier Transform. These windows taper the signal to zero at the boundaries, reducing discontinuities and minimizing leakage.

Mathematical Definition:

A windowed signal xw[n]x_w[n] is given by:

xw[n]=x[n]⋅w[n]x_w[n] = x[n] \cdot w[n]

where w[n]w[n] is the window function. For instance, a Hamming window is defined as:

w[n]=0.54−0.46cos⁡(2πnN−1),0≤n<Nw[n] = 0.54 – 0.46 \cos\left(\frac{2\pi n}{N-1}\right), \quad 0 \leq n < N

The choice of window affects the trade-off between main lobe width (frequency resolution) and side lobe level (leakage).

Example:

Applying a Hamming window to the previous example x[n]=cos⁡(2π532n)x[n] = \cos(2\pi \frac{5}{32} n) will reduce the side lobes in the spectrum, concentrating the energy around the main frequency component and providing a clearer representation of the signal’s frequency content.

4. Parseval’s Theorem

Parseval’s Theorem provides a relationship between the total energy of a signal in the time domain and the frequency domain. It states that the total energy of the signal is equal in both domains:

∑n=0N−1∣x[n]∣2=1N∑k=0N−1∣X[k]∣2\sum_{n=0}^{N-1} |x[n]|^2 = \frac{1}{N} \sum_{k=0}^{N-1} |X[k]|^2

This theorem is crucial for energy conservation in signal processing and helps verify the correctness of Fourier Transforms.

Example:

For a discrete signal x[n]={1,1,1,1}x[n] = \{1, 1, 1, 1\}, the total energy in the time domain is:

∑n=03∣x[n]∣2=1+1+1+1=4\sum_{n=0}^{3} |x[n]|^2 = 1 + 1 + 1 + 1 = 4

Calculating its DFT, the energy in the frequency domain is also found to be 4, demonstrating Parseval’s Theorem.

5. Convolution in the Frequency Domain

Convolution in the time domain corresponds to multiplication in the frequency domain. This property simplifies the filtering process, as applying a filter to a signal becomes a matter of multiplying their respective Fourier Transforms.

Mathematical Definition:

If x(t)x(t) and h(t)h(t) are two time-domain signals, their convolution y(t)y(t) is given by:

y(t)=x(t)∗h(t)=∫−∞∞x(τ)h(t−τ) dτy(t) = x(t) * h(t) = \int_{-\infty}^{\infty} x(\tau) h(t – \tau) \, d\tau

In the frequency domain, this becomes:

Y(f)=X(f)⋅H(f)Y(f) = X(f) \cdot H(f)

Example:

Let x(t)=cos⁡(2πf1t)x(t) = \cos(2\pi f_1 t) and h(t)h(t) be a low-pass filter with a cutoff frequency at fc=f1f_c = f_1. In the frequency domain, X(f)X(f) will be multiplied by H(f)H(f), resulting in a filtered signal that only retains the desired frequency components.

Frequency Domain Filtering Fundamentals

Frequency domain filtering involves manipulating the frequency components of a signal or image. This method is widely used in both signal and image processing to enhance, attenuate, or isolate specific frequencies.

Basic Concepts

Frequency Domain Representation
In the frequency domain, a signal is represented as a sum of sinusoidal components, each with a specific frequency, amplitude, and phase. The Fourier Transform (FT) is a mathematical tool used to transform a signal from the time or spatial domain into the frequency domain.

  • Fourier Transform (FT)
    For a continuous signal x(t)x(t), the Fourier Transform X(f)X(f) is defined as:

    X(f)=∫−∞∞x(t)e−j2πftdtX(f) = \int_{-\infty}^{\infty} x(t) e^{-j2\pi ft} dt

    Here, jj is the imaginary unit and ff represents frequency. The FT decomposes the signal into its frequency components.

  • Inverse Fourier Transform (IFT)
    To reconstruct the original signal from its frequency components, the Inverse Fourier Transform is used:

    x(t)=∫−∞∞X(f)ej2πftdfx(t) = \int_{-\infty}^{\infty} X(f) e^{j2\pi ft} df

  • Discrete Fourier Transform (DFT)
    For discrete signals, the Discrete Fourier Transform is used:

    X[k]=∑n=0N−1x[n]e−j2πNknX[k] = \sum_{n=0}^{N-1} x[n] e^{-j \frac{2\pi}{N} kn}

    where NN is the number of samples, and kk is the frequency index. The Fast Fourier Transform (FFT) is a computationally efficient algorithm for calculating the DFT.

Frequency Spectrum
The frequency spectrum of a signal provides information about the magnitude and phase of each frequency component:

  • Magnitude Spectrum: Shows the amplitude of each frequency component.
  • Phase Spectrum: Shows the phase shift associated with each frequency component.

Frequency Domain Filtering

Types of Filters
Different types of filters are used depending on the desired modification to the signal:

  • Low-Pass Filter (LPF): Allows low frequencies to pass and attenuates high frequencies. Useful for reducing noise and smoothing signals.
  • High-Pass Filter (HPF): Allows high frequencies to pass and attenuates low frequencies. Useful for edge detection and removing slow trends in signals.
  • Band-Pass Filter (BPF): Allows a specific range of frequencies to pass and attenuates frequencies outside this range. Used for isolating signals within a certain frequency range.
  • Band-Stop Filter (BSF) or Notch Filter: Attenuates a specific range of frequencies and allows others to pass. Used to eliminate unwanted frequencies, such as power line interference.

Filtering Process

  1. Transform the Signal to the Frequency Domain
    Convert the signal from the time or spatial domain to the frequency domain using the Fourier Transform.

  2. Apply the Filter in the Frequency Domain
    Multiply the frequency spectrum of the signal X(f)X(f) by the filter’s transfer function H(f)H(f). This operation modifies the amplitude and phase of specific frequencies:

    Y(f)=X(f)⋅H(f)Y(f) = X(f) \cdot H(f)

  3. Transform Back to the Time Domain
    Convert the filtered signal back to the time domain using the Inverse Fourier Transform.

Example: Low-Pass Filtering

Problem Statement:
Consider a discrete signal x[n]=[1,2,3,4,3,2,1,0]x[n] = [1, 2, 3, 4, 3, 2, 1, 0]. We want to apply a low-pass filter to remove high-frequency components.

  1. Compute the DFT of the Signal:
    Calculate the DFT of x[n]x[n] to obtain its frequency representation X[k]X[k].

  2. Design a Low-Pass Filter:
    Create a filter transfer function H[k]H[k] that retains only the low-frequency components:

    H[k]={1if k≤20if k>2H[k] = \begin{cases} 1 & \text{if } k \leq 2 \\ 0 & \text{if } k > 2 \end{cases}

  3. Apply the Filter:
    Multiply the DFT of the signal by the filter:

    Y[k]=X[k]⋅H[k]Y[k] = X[k] \cdot H[k]

  4. Compute the Inverse DFT:
    Convert Y[k]Y[k] back to the time domain using the inverse DFT to obtain the filtered signal y[n]y[n].

Interpretation
The low-pass filter smooths the signal by removing rapid changes, which correspond to high frequencies. This results in a smoother version of the original signal.

Applications of Frequency Domain Filtering

  • Image Processing: Used for tasks like noise reduction, image enhancement, and edge detection.
  • Signal Processing: Useful in applications such as audio signal enhancement, communication signal filtering, and noise removal.
  • Biomedical Signal Processing: Used to remove specific interference, like power line noise, from ECG signals.
Frequency Domain Filtering Fundamentals
(a) Original filter specified in the (centered) frequency domain. (b) Spatial representation obtained by computing the IDFT of (a). (c) Result of padding (b) to twice its length (note the discontinuities). (d) Corresponding filter in the frequency domain obtained by computing the DFT of (c).Note the ringing caused by the discontinuities in (c).(The curves appear continuous because the points were joined to simplify visual analysis.)

References

  1. Oppenheim, A. V., & Schafer, R. W. (2009). Discrete-Time Signal Processing (3rd ed.). Pearson Education.
  2. Proakis, J. G., & Manolakis, D. G. (2006). Digital Signal Processing: Principles, Algorithms, and Applications (4th ed.). Pearson Education.
  3. Smith, S. W. (1997). The Scientist and Engineer’s Guide to Digital Signal Processing. California Technical Publishing.
  4. Bracewell, R. N. (2000). The Fourier Transform and Its Applications (3rd ed.). McGraw-Hill Education.
  5. Lyons, R. G. (2010). Understanding Digital Signal Processing (3rd ed.). Pearson Education.

Leave a Comment