Using Fuzzy Techniques for Intensity Transformations and Spatial Filtering

1. Fundamentals of Fuzzy Logic

Fuzzy logic extends classical Boolean logic by introducing the concept of partial truth values between 0 and 1. This allows for a more nuanced representation of information, where an element can partially belong to a set.

1.1. Membership Functions

A membership function $\mu : X \rightarrow [0, 1]$ assigns a degree of membership to each element in a set $X$. For example, in the context of image processing, we might define a fuzzy set of “bright pixels” with a membership function that assigns higher values to brighter pixels.

2. Fuzzy Intensity Transformations

Intensity transformations are used to modify the pixel values of an image to enhance its appearance or to highlight certain features. Fuzzy techniques can be particularly effective in dealing with images with varying illumination and contrast conditions.

2.1. Fuzzy Histogram Equalization

Fuzzy histogram equalization improves the contrast of an image by redistributing the intensity values more evenly. Unlike traditional histogram equalization, which uses crisp intensity values, fuzzy histogram equalization uses fuzzy sets and membership functions.

1. Fuzzification: Convert the image intensity values into fuzzy sets using membership functions.

   $\mu_A(x) = \frac{1}{1 + \left(\frac{x – c}{b}\right)^2}$

   where $\mu_A(x)$ is the membership value of intensity $x$, $c$ is the center of the fuzzy set, and $b$ is the width of the fuzzy set.

2. Equalization: Apply histogram equalization on the fuzzy membership values.

   $\mu_A'(x) = \text{CDF}(\mu_A(x))$

   where $\text{CDF}$ is the cumulative distribution function of the fuzzy membership values.

3. Defuzzification: Convert the fuzzy membership values back to intensity values.

   $x’ = c + b \cdot \sqrt{\frac{1}{\mu_A'(x)} – 1}$

2.2. Fuzzy Contrast Stretching

Fuzzy contrast stretching enhances the contrast of an image by stretching the range of the fuzzy membership values.

1. Fuzzification: Convert intensity values to fuzzy sets as before.

2. Stretching: Apply a linear transformation to the fuzzy membership values.

   $\mu_A'(x) = a \cdot \mu_A(x) + b$

   where $a$ and $b$ are stretching parameters.

3. Defuzzification: Convert the stretched fuzzy membership values back to intensity values using the inverse of the fuzzification function.

3. Fuzzy Spatial Filtering

Spatial filtering modifies the spatial structure of an image to enhance features or reduce noise. Fuzzy techniques allow for more adaptive and context-sensitive filtering.

3.1. Fuzzy Smoothing Filters

Fuzzy smoothing filters reduce noise while preserving edges by considering the local context of each pixel.

1. Fuzzification: Convert the neighborhood of each pixel into fuzzy sets using membership functions.

2. Fuzzy Aggregation: Compute a weighted average of the fuzzy membership values in the neighborhood.

   $\mu_A'(x, y) = \sum_{(i,j) \in N(x,y)} w_{ij} \cdot \mu_A(i, j)$

   where $N(x, y)$ is the neighborhood of pixel $(x, y)$, and $w_{ij}$ are weights based on the spatial distance from $(x, y)$.

3. Defuzzification: Convert the aggregated fuzzy membership values back to intensity values.

3.2. Fuzzy Edge Detection

Fuzzy edge detection enhances the edges in an image by considering the gradient magnitude and direction in a fuzzy manner.

1. Fuzzification: Compute the gradient magnitude and direction for each pixel and convert them into fuzzy sets.

   $\mu_A(g) = \frac{1}{1 + \left(\frac{g – g_0}{\sigma}\right)^2}$

   where $g$ is the gradient magnitude, $g_0$ is a reference gradient magnitude, and $\sigma$ controls the spread of the fuzzy set.

2. Fuzzy Inference: Use fuzzy rules to infer the presence of edges based on the gradient magnitude and direction.

   $\mu_E(x, y) = \max \left( \mu_A(g_x) \cdot \mu_A(g_y) \right)$

   where $\mu_E(x, y)$ is the fuzzy edge membership value at pixel $(x, y)$.

3. Defuzzification: Convert the fuzzy edge membership values back to intensity values to obtain the edge-enhanced image.

4. Combining Fuzzy Techniques

Combining fuzzy intensity transformations and spatial filtering can lead to more robust and adaptive image enhancement. Here is a typical procedure:

1. Fuzzification: Convert the original image intensity values to fuzzy sets.

   $\mu_A(x, y) = \frac{1}{1 + \left(\frac{I(x, y) – c}{b}\right)^2}$

2. Fuzzy Intensity Transformation: Apply fuzzy histogram equalization or fuzzy contrast stretching.

3. Fuzzy Spatial Filtering: Apply fuzzy smoothing or edge detection to the transformed fuzzy sets.

4. Defuzzification: Convert the processed fuzzy membership values back to intensity values.

   $I'(x, y) = c + b \cdot \sqrt{\frac{1}{\mu_A'(x, y)} – 1}$

Fuzzy set theory, introduced by Lotfi Zadeh in 1965, extends classical set theory to handle the concept of partial truth, where an element’s membership in a set can range between complete membership and complete non-membership. This framework is particularly useful in dealing with uncertain, imprecise, or vague information, and has applications in various fields including control systems, decision making, and artificial intelligence.

Basic Concepts

Fuzzy Sets: A fuzzy set $A$ in a universe of discourse $X$ is characterized by a membership function $\mu_A : X \to [0, 1]$. This function assigns each element $x \in X$ a membership value $\mu_A(x)$ within the interval $[0, 1]$, where 0 indicates no membership and 1 indicates full membership.

Example: Consider the set of “tall people”. In classical set theory, a person either belongs to the set of tall people or not. In fuzzy set theory, each person has a degree of membership to the set of tall people based on their height. For instance, if $x$ is a person with a height of 180 cm, the membership function $\mu_{\text{tall}}(x)$ might assign a value of 0.8, indicating that this person is “mostly tall”.

Membership Functions

The choice of membership function is critical in fuzzy set theory. Common types of membership functions include:

1. Triangular Membership Function: Defined by three parameters $a$, $b$, and $c$ where $a < b < c$. The function is given by:

   $$\mu_A(x) = \begin{cases} 0 & \text{if } x \le a \text{ or } x \ge c, \\ \frac{x-a}{b-a} & \text{if } a < x < b, \\ \frac{c-x}{c-b} & \text{if } b < x < c. \end{cases}$$

2. Trapezoidal Membership Function: Defined by four parameters $a$, $b$, $c$, and $d$ where $a < b < c < d$. The function is given by:

   $$\mu_A(x) = \begin{cases} 0 & \text{if } x \le a \text{ or } x \ge d, \\ \frac{x-a}{b-a} & \text{if } a < x < b, \\ 1 & \text{if } b \le x \le c, \\ \frac{d-x}{d-c} & \text{if } c < x < d. \end{cases}$$

3. Gaussian Membership Function: Defined by the parameters $c$ (mean) and $\sigma$ (standard deviation). The function is given by:

   $$\mu_A(x) = e^{-\frac{(x-c)^2}{2\sigma^2}}.$$

Operations on Fuzzy Sets

Fuzzy set theory generalizes classical set operations to handle degrees of membership.

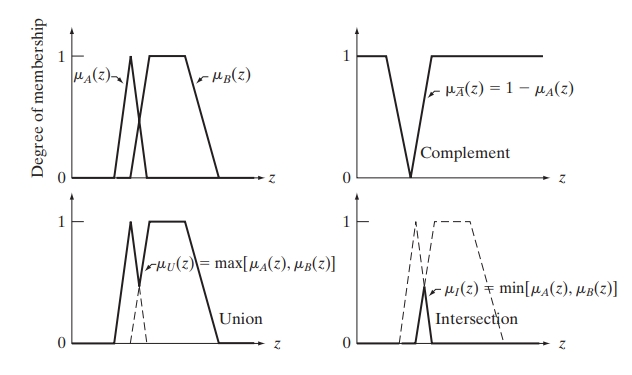
1. Union: The membership function of the union of two fuzzy sets $A$ and $B$ is given by:

   $$\mu_{A \cup B}(x) = \max(\mu_A(x), \mu_B(x)).$$

2. Intersection: The membership function of the intersection of two fuzzy sets $A$ and $B$ is given by:

   $$\mu_{A \cap B}(x) = \min(\mu_A(x), \mu_B(x)).$$

3. Complement: The membership function of the complement of a fuzzy set $A$ is given by:

   $$\mu_{\neg A}(x) = 1 – \mu_A(x).$$

Fuzzy Relations

Fuzzy relations extend the concept of classical relations to fuzzy sets. A fuzzy relation $R$ between two fuzzy sets $A$ and $B$ in the universes of discourse $X$ and $Y$ is characterized by a membership function $\mu_R : X \times Y \to [0, 1]$.

Composition of Fuzzy Relations: Given two fuzzy relations $R$ and $S$, the composition $R \circ S$ is defined by:

Fuzzy Logic

Fuzzy logic is an extension of Boolean logic that deals with reasoning that is approximate rather than fixed and exact. In fuzzy logic, truth values are expressed as degrees of truth ranging between 0 and 1. Fuzzy logic uses linguistic variables, which are described by fuzzy sets.

Fuzzy Inference Systems (FIS): These systems use fuzzy set theory and fuzzy logic to map inputs to outputs. An FIS consists of three main components:

1. Fuzzification: Converts crisp inputs into fuzzy sets.
2. Inference Engine: Applies fuzzy rules to the fuzzy inputs to generate fuzzy outputs.
3. Defuzzification: Converts fuzzy outputs back into crisp values.

Example: Consider a simple FIS for controlling the temperature of a room:

• Input: Current temperature (crisp value).
• Fuzzification: Transform the current temperature into fuzzy sets such as “cold”, “warm”, “hot”.
• Inference: Apply fuzzy rules like “If the temperature is cold, then increase the heater” to determine the output fuzzy set.
• Defuzzification: Convert the output fuzzy set back to a crisp value, which determines the heater setting.

Applications of Fuzzy Set Theory

Fuzzy set theory has numerous practical applications, including:

1. Control Systems: Used in various control systems, such as air conditioning, washing machines, and automotive systems, to handle imprecise inputs and provide smooth control actions.
2. Decision Making: Helps in multi-criteria decision making where criteria and their importance are not precisely defined.
3. Pattern Recognition: Used in image processing and pattern recognition to classify objects with imprecise boundaries.
4. Artificial Intelligence: Enhances AI systems by allowing them to deal with uncertainty and partial truths, improving decision-making processes in expert systems.

Fuzzy set theory provides a powerful tool for modeling and reasoning with uncertain, imprecise, or vague information. By extending classical set theory, it offers a flexible framework that can be applied to a wide range of real-world problems, enabling more nuanced and effective solutions. Its mathematical foundations, characterized by the use of membership functions and fuzzy logic, make it a vital component of modern computational intelligence and decision-making systems.

Intensity transformations are fundamental in image processing, aiming to enhance or modify the visual appearance of images. These transformations adjust the pixel intensity values to achieve better contrast, highlight certain features, or prepare images for further analysis. Fuzzy set theory provides a robust framework for handling the uncertainty and vagueness inherent in image data, enabling more nuanced and flexible intensity transformations.

Basic Concepts

Fuzzy Sets: In the context of image processing, a fuzzy set $A$ can be used to represent a specific range of pixel intensities in a grayscale image. The membership function $\mu_A : [0, 255] \to [0, 1]$ assigns each intensity value a membership degree, indicating how strongly that intensity belongs to the fuzzy set $A$.

Example: For an image with intensity values ranging from 0 (black) to 255 (white), a fuzzy set $A$ might represent “dark” pixels. The membership function $\mu_A(i)$ could assign higher values to lower intensities (closer to 0) and lower values to higher intensities (closer to 255).

Membership Functions in Intensity Transformations

Various types of membership functions can be utilized to model different intensity levels:

1. Triangular Membership Function:

   $$\mu_A(i) = \begin{cases} 0 & \text{if } i \le a \text{ or } i \ge c, \\ \frac{i-a}{b-a} & \text{if } a < i < b, \\ \frac{c-i}{c-b} & \text{if } b < i < c. \end{cases}$$

   Here, $a$, $b$, and $c$ define the shape of the triangle, where $a$ and $c$ are the endpoints, and $b$ is the peak.

2. Gaussian Membership Function:

   $$\mu_A(i) = e^{-\frac{(i-c)^2}{2\sigma^2}}.$$

   This function is defined by the mean $c$ and the standard deviation $\sigma$, providing a smooth bell-shaped curve.

3. Trapezoidal Membership Function:

   $$\mu_A(i) = \begin{cases} 0 & \text{if } i \le a \text{ or } i \ge d, \\ \frac{i-a}{b-a} & \text{if } a < i < b, \\ 1 & \text{if } b \le i \le c, \\ \frac{d-i}{d-c} & \text{if } c < i < d. \end{cases}$$

   Defined by $a$, $b$, $c$, and $d$, this function creates a trapezoid shape, which is useful for representing intensity ranges with a flat top.

Fuzzy Intensity Transformation Process

The process of using fuzzy sets for intensity transformations involves several key steps:

1. Fuzzification: Convert the pixel intensities of the image into fuzzy values using a suitable membership function. This step maps each intensity value $i$ to a membership degree $\mu_A(i)$.

2. Application of Fuzzy Rules: Apply a set of fuzzy rules to modify the fuzzy membership values. These rules can be designed to enhance contrast, highlight certain intensity ranges, or achieve other desired effects.

3. Defuzzification: Convert the modified fuzzy membership values back into crisp intensity values. This step maps the fuzzy values to new intensity values, resulting in the transformed image.

Example: Contrast Enhancement

Let’s consider a simple example of using fuzzy sets for contrast enhancement in a grayscale image.

1. Fuzzification: Define a fuzzy set $A$ to represent “dark” pixels and another fuzzy set $B$ to represent “bright” pixels. For simplicity, use triangular membership functions for both sets:

   $$\mu_A(i) = \begin{cases} 1 – \frac{i}{128} & \text{if } 0 \le i \le 128, \\ 0 & \text{if } i > 128. \end{cases}$$ $$\mu_B(i) = \begin{cases} 0 & \text{if } i < 128, \\ \frac{i – 128}{128} & \text{if } 128 \le i \le 255. \end{cases}$$

2. Application of Fuzzy Rules: Define fuzzy rules to enhance contrast:

   • Rule 1: If a pixel is dark, make it darker.
   • Rule 2: If a pixel is bright, make it brighter.

   These rules can be implemented by adjusting the membership functions. For instance:

   $$\mu_{A’}(i) = \mu_A(i) \cdot (1 – \alpha), \quad \text{where } 0 < \alpha < 1,$$ $$\mu_{B’}(i) = \mu_B(i) \cdot (1 + \beta), \quad \text{where } \beta > 0.$$

3. Defuzzification: Convert the modified membership values back to crisp intensity values. One common method is the centroid method, which calculates the center of gravity of the membership function:

   $$i’ = \frac{\sum_{i=0}^{255} i \cdot \mu_{A’}(i)}{\sum_{i=0}^{255} \mu_{A’}(i)}.$$

   Apply the same process for the modified fuzzy set $B’$:

   $$j’ = \frac{\sum_{i=128}^{255} i \cdot \mu_{B’}(i)}{\sum_{i=128}^{255} \mu_{B’}(i)}.$$

   Replace the original pixel intensities with the defuzzified values to get the enhanced image.

Practical Considerations

Choosing Membership Functions: The choice of membership functions significantly impacts the effectiveness of the intensity transformation. Triangular, trapezoidal, and Gaussian functions are commonly used due to their simplicity and ease of computation.

Defuzzification Methods: While the centroid method is widely used, other defuzzification methods such as the mean of maxima (MOM) or the smallest of maxima (SOM) can also be applied, depending on the specific requirements of the application.

Computational Complexity: Fuzzy intensity transformations can be computationally intensive, especially for large images. Efficient algorithms and parallel processing techniques can help mitigate this issue.

Applications

Fuzzy set-based intensity transformations have various applications in image processing:

1. Medical Imaging: Enhancing the contrast of medical images (e.g., X-rays, MRI scans) to highlight specific tissues or abnormalities.
2. Remote Sensing: Improving the visibility of features in satellite or aerial images for better analysis and interpretation.
3. Surveillance: Enhancing the visibility of objects or individuals in surveillance footage under varying lighting conditions.
4. Photography: Adjusting the contrast and brightness of digital photographs to achieve desired artistic effects.

Using fuzzy sets for intensity transformations provides a powerful and flexible approach to image enhancement. By incorporating the concepts of fuzzy membership and fuzzy rules, this method can handle the inherent uncertainty and vagueness in image data, resulting in more effective and adaptive transformations. The mathematical framework of fuzzy set theory, combined with practical considerations, makes it a valuable tool in the field of image processing.